The Carnot cycle is entropy, the second law of thermodynamics. Second law of thermodynamics

12.09.2024

2.3.1. Reversible and circular processes

Reversible process is a process that can be carried out in the opposite direction in such a way that the system will pass through the same thermodynamic states as in the forward process, but in the reverse order. Only an equilibrium process can be reversible.

A reversible process has the following property: if during a forward stroke in some elementary section the system receives heat dQ and does work dA, then during a reverse stroke in the same section the system gives off heat dQ" = dQ and above her work is done dA" = dA. For this reason, after the reversible process occurs in one and then in the opposite direction and the system returns to its original state, no changes should occur in the bodies surrounding the system.

Circular process (cycle) is a process in which a system, after a series of changes, returns to its original state. On the graph, the cycle is depicted as a closed curve (Fig. 2.3.1).

Rice. 2.3.1. Circular thermodynamic process

The work done in a circular process is numerically equal to the area covered by the curve. Indeed, the work in section 1-2 is positive and is numerically equal to the area marked by the hatching inclined to the right. The work in area 2-1 is negative and is numerically equal to the area marked by hatching inclined to the left. Therefore, the work per cycle is numerically equal to the area covered by the curve.

After completing the cycle, the system returns to its original state.

2.3.2. Efficiency factor
action of a heat engine

Every engine is a system that repeatedly performs some circular process (cycle). Suppose that during the cycle the working substance (for example, gas) first expands to volume V 2 and then contracts again to the original volume V 1 (Fig. 2.3.2).

Rice. 2.3.2. To calculate the efficiency of a heat engine

In order for the work per cycle to be greater than zero, the pressure (and, therefore, temperature) during the expansion process must be greater than during compression. To do this, heat must be added to the working substance during expansion, and heat must be removed from it during compression.

Let's write the first law of thermodynamics for both parts of the cycle. During expansion, the internal energy changes from the value U 1 to U 2, while the system receives heat Q 1 and does work A 1. Therefore it runs:

During compression, the system performs work A 2 and gives off heat Q 2, which is equivalent to receiving heat Q 2. Hence,

Adding equations (2.3.1) and (2.3.2), we obtain:

Since A 1 + A 2 is the total work A performed by the system per cycle, we can write:

A periodically operating engine that performs work using heat received from outside is called heat engine.

The first law of thermodynamics is sometimes formulated as follows: a periodically operating perpetual motion machine (perpetuum mobile) of the first kind, performing work in greater quantities than it receives energy from the outside, impossible.

As follows from (2.3.4), not all heat Q 1 received from outside is used to produce useful work. In order for the engine to operate in cycles, part of the heat Q 2 must be returned to the external environment and, therefore, is not used for its intended purpose. Obviously, the more completely a heat engine converts heat Q 1 received from outside into useful work A, the more profitable this machine is. Therefore, a heat engine is usually characterized by its coefficient of performance (efficiency), which is defined as the ratio of the work performed per cycle to the amount of heat received per cycle Q 1:

From the definition of efficiency it follows that it cannot be greater than one.

2.3.3. Second law of thermodynamics

The second law of thermodynamics, like the first, can be formulated in several ways. In its most obvious formulation, the second law states that:

Spontaneous transfer of heat from a less heated body to a more heated body is impossible. More strictly, such processes are impossible, the only final result of which would be the transfer of heat from a body that is less heated to a body that is more heated.

Another formulation: such processes are impossible, the only final result of which would be the removal of a certain amount of heat from a certain body and the complete conversion of this heat into work.

Work can be completely converted into heat, for example, by friction, the reverse is not true.

2.3.4. Carnot cycle

Let us assume that any body can enter into heat exchange with two heat reservoirs having temperatures T 1 and T 2 and having an infinitely large heat capacity. This means that the receipt or release of a finite amount of heat by these reservoirs does not change their temperature. Let's find out what reversible cycle a body can perform under such conditions.

The cycle under consideration can consist of both processes during which the body exchanges heat with reservoirs, and processes that are not accompanied by heat exchange with the environment, i.e. occurring adiabatically.

A process accompanied by the exchange of heat with reservoirs can be reversible only if during this process the body temperature is equal to the temperature of the corresponding reservoir. This is an isothermal process occurring at tank temperature.

A reversible cycle performed by a body (or system) entering into heat exchange with two thermal reservoirs of infinitely large capacity will consist of two isotheres (at the temperatures of the reservoirs) and two adiabats. This - Carnot cycle.

Let's consider how the Carnot cycle can be implemented with gas as a working substance. Let's place the gas in a cylinder closed with a tightly fitting piston. Let the walls and piston be made of non-heat-conducting materials; the bottom of the cylinder, on the contrary, is made of a material with high thermal conductivity. The heat capacity of the cylinder and piston is considered infinitesimal.

Let the piston initially take a position corresponding to the volume V 1 and gas temperature T 1 . Let's place the cylinder on a tank having a temperature T 1 and allow the gas to expand very slowly to a volume V 2 . In this case, the gas will receive heat Q 1 from the reservoir (Fig. 2.3.3).

Rice. 2.3.3. Heat engine operating on the Carnot cycle

Then we remove the cylinder from the tank, close the bottom with a heat-insulating lid and allow the gas to expand adiabatically until its temperature drops to the value T 2. As a result, the volume of gas will become equal to V 3. Having removed the heat-insulating cover, we place the cylinder on a tank having a temperature T 2 and compress the gas isothermally to such a volume V 4 that upon subsequent adiabatic compression, when the temperature T 1 is reached, the volume receives the value V 1 (otherwise the cycle will not close). Finally, we remove the cylinder from the tank, close the bottom with a heat-insulating lid and, compressing the gas adiabatically, bring it to its original state (temperature T 1, volume V 1).

If the gas is ideal, the corresponding cycle on the (p-V) diagram has the form shown in Fig. 2.3.4.

Rice. 2.3.4. (p-V) Carnot cycle diagram

2.3.5. Efficiency of the Carnot cycle for an ideal gas

Consider the Carnot cycle for an ideal gas. The efficiency of a heat engine is:

where Q 1 is the heat received per cycle from the heater, Q 2 is the heat given off to the refrigerator per cycle.

In an isothermal process, the internal energy of an ideal gas remains constant. Therefore, the amount of heat Q1 received by the gas is equal to the work A12 performed by the gas during the transition from state 1 to state 2 (Fig. 2.3.4). This work can be calculated as follows:

Using the Clapeyron-Mendeleev equation, we obtain:

where m is the mass of an ideal gas in a heat engine.

The amount of heat Q 2 given off to the refrigerator is equal to the work A 34 spent on compressing the gas when transferring it from state 3 to state 4. This work is equal to:

In order for the cycle to be closed, states 4 and 1 must lie on the same adiabat. From here, using (2.1.68) we can obtain:

Similarly, since states 2 and 3 lie on the same adiabat, the following holds:

Dividing (2.3.11) by (2.3.10), we arrive at the condition for the cycle to be closed:

Finally, taking into account condition (2.3.12), for the efficiency of a heat engine operating according to the Carnot cycle for an ideal gas, we obtain:

Consequently, the efficiency of the Carnot cycle for an ideal gas turns out to depend only on the temperature of the heater and refrigerator.

Even for the best heat engine operating according to the Carnot cycle, the efficiency is always significantly less than unity. If, for example, the heater temperature T 1 = 373 K (boiling point of water), and the refrigerator temperature T 2 = 293 K (room temperature), then η = 22%. And this efficiency is the upper (and unattainable) limit. In real machines, for example, on steam locomotives, it rarely exceeded 10%.

2.3.6. Entropy

Let us pay attention to the changes that the working fluid underwent during the circular Carnot cycle. From the initial state 1 (pressure p 1, temperature T 1), the working fluid, through sequential isothermal and adiabatic expansions, passed into state 3, when it assumed the temperature of the refrigerator T 2. This change in state occurred due to the heat Q 1 delivered to the working fluid by the heater. The reverse transition of the working fluid from state 3 to the initial state 1 was carried out by two successive isothermal and adiabatic compressions of the body. The amount of heat released during this return to the original state is equal to Q 2, and Q 2< Q 1 . Таким образом, оказывается, что обратимый переход одного и того же тела из состояния 1 → 3 и обратный переход 3 → 1 сопровождаются неодинаковыми количествами поглощенного и выделенного тепла. Очевидно, что это связано с тем, что оба перехода были проведены различными путями: в одном случае (1 → 3) процесс расширения происходил при давлении более высоком, чем процессы сжатия в другом (3 → 1). Ясно, что если бы мы осуществили переход 3 → 1 тем же путем, что и прямой, т.е. по кривой 3 → 2 → 1, а не по кривой 3 → 4 → 1 (), то количество тепла, затраченного при прямом переходе, в точности равнялось бы количеству тепла, выделившемуся при обратном переходе.

An important conclusion follows from this: the amount of heat that must be delivered to the body or taken away from it during the transition from one state to another is not uniquely determined by the initial and final states, but significantly depends on the method of carrying out this transition.

However, although the amounts of heat themselves - Q 1 delivered to the working body by the heater at temperature T 1, and Q 2 transferred by the working body to the refrigerator at temperature T 2 - are not equal to each other, as follows from a comparison of formulas (), () and (), the ratios of these heats to the temperatures at which they were absorbed or released are numerically equal to each other (but have opposite signs):

The relation is called, following Lorentz, reduced heat. From (2.3.15) it follows that the reduced heats received and transferred by the working fluid during a circular process are equal to each other.

Let us generalize this result. In the general case, any change in the state of a body or system of bodies can be represented as the result of an infinitely large number of infinitesimal changes. For each such infinitesimal change, the system either absorbs or releases an infinitesimal amount of heat dQ (if the process is not adiabatic). Let dQ > 0 when the system absorbs heat. where dQ is the amount of heat removed from the body M at temperature T, dQ" is the amount of heat transferred to the reservoir at temperature T 1.

If T 1< T, резервуар играет роль холодильника, а тело М - нагревателя, и наоборот.

After the body M completes the circular process, the total amount of heat lost by the body, as follows from (2.3.17), must be equal to . Since the heat capacity of the reservoir is large and its temperature remains constant, this value will be equal to: .

The process performed by the body is circular. Therefore, it did not experience any changes in the end. If the integral (2.3.16) turned out to be positive, then this would mean that the amount of heat lost by the body was entirely converted into work, while the body M did not change its state. However, this contradicts the second law of thermodynamics. This means that the assumption that . Similarly, it can be shown that the indicated integral cannot be negative. But if it can be neither positive nor negative, then this means that for reversible circular processes the following holds:

The entropy of an isolated system can only increase (if an irreversible process occurs in the system), or remain constant in the case of a reversible process.

Nernst proved a theorem (sometimes called the third law of thermodynamics), according to which, as the absolute temperature tends to zero, the entropy of any body also tends to zero:

Then the entropy of the state of the body at temperature T can be calculated as follows.

Second law of thermodynamics– heat cannot spontaneously transfer from a less heated body to a more heated body. Heat refers to the internal energy of a body.

Consider a system capable of contacting two thermal reservoirs. Tank temperatures (heater) And (fridge).. In the initial state (item 1), the system temperature is . Let's bring it into thermal contact with the heater and, quasi-statically reducing the pressure, increase the volume.

The system switched to a state with the same temperature, but with a larger volume and lower pressure (position 2). At the same time, the system performed work, and the heater transferred an amount of heat to it. Next, we remove the heater and quasi-statically adiabatically transfer the system to a state with temperature (item 3). In this case, the system will perform the work. Then we bring the system into contact with the refrigerator and statically reduce the volume of the system. The amount of heat that the system will release will be absorbed by the refrigerator - its temperature will remain the same. Work has been done on the system (or the system has done negative work – ). The state of the system (item 4) is selected such that it is possible to adiabatically return the system to its original state (item 1). In this case, the system will perform negative work. the system returned to its original state, then the internal energy after the cycle remained the same, but work was done by the system. It follows that changes in energy during work were compensated by the heater and refrigerator. Means , is the amount of heat that went into doing the work. Efficiency (efficiency) is determined by the formula:

It follows that .

Carnot's theorem states that The efficiency coefficient of a heat engine operating according to the Carnot cycle depends only on the temperatures of both the heater and refrigerator, but does not depend on the design of the machine, as well as on the type of working substance.

Carnot's second theorem reads: the efficiency coefficient of any heat engine cannot exceed the efficiency coefficient of an ideal machine operating according to the Carnot cycle with the same temperatures of the heater and refrigerator.

Clausius inequality:

It shows that the amount of heat that the system received during a circular process, related to the absolute temperature at which the process occurred, is a non-positive quantity. If the process is quasi-static, then the inequality turns into equality:

This means that the reduced amount of heat received by the system during any quasi-static circular process is equal to zero .

– elementary reduced amount of heat received in infinitely

small process.

– elementary reduced amount of heat received in the final

process.

Entropy of the system There is a function of its state, defined up to an arbitrary constant.

Entropy difference in two equilibrium states and, by definition, is equal to the reduced amount of heat that must be imparted to the system in order to transfer it from state to state along any quasi-static path.

Entropy is expressed by the function:

Let us assume that the system transitions from an equilibrium state to an equilibrium state along the path , and the transition is irreversible (shaded line). A quasi-static system can be returned to its original state via another path. Based on the Clausius inequality, we can write:

For any heat engine to operate in a closed cycle, an external environment is required, which can be conventionally imagined as two bodies - heater T max, And fridge, located at temperature T min(T min< Т mах ). It is assumed that the temperatures of the heater and refrigerator do not change when in contact with our system. When it comes into contact with the heater, the system receives heat, and when it comes into contact with the refrigerator, it releases it.

In thermodynamics there is Carnot's theorem(Fig. 5.2):

Rice. 5.2. Leonard Sadi Carnot (French physicist and military engineer)

At given temperatures of the heater and refrigerator, the maximum possible efficiency of a heat engine does not depend on the nature of the working fluid of the machine and is determined by the formula

The implementation of the maximum possible efficiency is achieved in the so-called Carnot cycle, when an ideal gas goes through a closed cycle composed of two adiabats and two isotherms (Fig. 5.3).

Rice. 5.3.Carnot cycle (clockwise)- combination of two isotherms 1- 2, 3 - 4 and two adiabats 2- 3 and 4- 1 ; heat exchange with the environment is carried out on isothermal areas cycle: in section 1- 2 gas receives heatQ 1 , and in section 3- 4 gives off heatQ 2

Let us make sure that the shown closed process actually has an efficiency corresponding to formula (5.5). The system temperature is T 1 at points 1, 2 And T 2 at points 3, 4 . Values of other thermodynamic parameters (p, V) will have as an index the number of the corresponding point on the diagram. We need to calculate the quantities received Q 1, and given Q 2 heat, find the work done by the gas A C = Q 1 – Q 2 and determine the cycle efficiency. Let us immediately note that in areas 2-3 And 4-1 the system does not exchange heat with the external environment. Therefore, the heat Q 1 receives gas at the site 1-2, and warmth Q 2 gives away at the site 3-4. Let's take a closer look at the different sections of the cycle.

Isotherm 1 -2. In this section, the gas is in contact with the heater and isothermal expansion from the volume occurs V 1 up to volume V 2. Temperature T 1 does not change, therefore, the internal energy does not change, and all the heat received is spent on doing work by the gas:

We have already calculated the amount of work done by a gas during an isothermal process, so taking into account the formula (2.13) we find

Adiabata 2 -3. Here the system is disconnected from the heater and does not exchange heat with the external environment: Q23 = 0. The gas continues to expand, but now adiabatically. Work is done due to the internal energy of the gas, and its temperature drops to the value T 2. At this point in the cycle we need information delivered adiabatic equation:

Isotherm 3 -4. The system is connected to the refrigerator, and the gas begins to be compressed. The internal energy remains unchanged, work is done on the gas ( A 34< 0 ), and the standout

transferred to the refrigerator. We have similarly (5.6)

Adiabata 4 -1. The system is disconnected from the external environment and continues to compress isothermally, which leads to an increase in its temperature to T 1. Ultimately, the system returns to its original state. Since the points 4 And 1 lie on the adiabat, we obtain a relationship between volumes and temperatures similar to (5.7):

From equations (5.7) and (5.9) we find the volume ratios

whence it follows that

Therefore, the heat transferred to the refrigerator Q 2(see equation (5.8)) can be written as

Using expression (5.6) for the heat received by the system, we find the work done during the cycle

From the analysis it also follows that the maximum temperature in the cycle is equal to T max = T 1, and the minimum - T min = T 2. If we divide (5.12) by (5.6), we immediately obtain expression (5.5) for the efficiency of the Carnot cycle, from which all parameters drop out except the temperatures of the refrigerator and heater.

Example 1. The thermal station boiler operates at a temperature of approx. t 1 = 550 °C. The waste heat is transferred to the river at a temperature of about t 2 = 20 °C. Let's find the maximum possible efficiency of this station (Fig. 5.4).

Rice. 5.4. Diagram of operation of a Carnot heat engine

Since the formula for the efficiency of the Carnot cycle uses absolute temperatures, we must move from the Celsius scale to the Kelvin scale: T 1 = 550 + 273 = 823 K, T 2 = 20 + 273 = 293 K. Now we find the efficiency of the thermal station:

Of course, the real efficiency of the station is noticeably lower.

If the Carnot cycle is carried out in the opposite direction, that is, counterclockwise in Fig. 5.2, then to determine the efficiency of the refrigeration unit it is necessary to use formulas (5.3), (5.4) and expressions (5.6), (5.11). Then we get

It's sad, but the lower the ambient temperature T 1, the less we need a refrigerator, and the more efficiently it works.

Rice. 5.5. Refrigeration unit operation diagram

Let's give a numerical example. If the air conditioner maintains the temperature in the room t 2 = 20 °C, and the outside air temperature is t 1 = 30 °C, then for the coefficient of performance we have

and for the efficiency of the refrigerator

Of course, in fact, the temperature of the fuel element is 20–30 degrees higher than the outside temperature, so the temperature difference can reach 30–40 degrees, which leads to values

Let us recall that we are talking about ideal installations operating according to the Carnot cycle. Real Typical Air Conditioner Power Consumes 750 W, pumping in about an hour 5 MJ thermal energy. This means that in a second the air conditioner does work A = 750 J and takes heat away from the air in the room

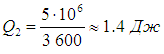
From here we find

We see that a real air conditioner is much less efficient than an ideal Carnot refrigerator.

Example 2. Keep your home refrigerator at temperature t 2 = –3 °С (T 2 = 270 K), and the temperature in the kitchen is t 1 = 27 °C (T 1 = 300 K). Let the refrigerator motor continue to consume power N = 200 W. Assuming that the refrigerator operates according to the Carnot cycle and that the fuel element is at ambient temperature, we will determine the power of the flow of thermal energy pumped from the refrigerator chamber to the kitchen.

During the time t the motor will do the work

The efficiency of the refrigerator is

from where we find the amount of heat entering the kitchen per unit time:

Please note that the refrigerator operates as a very efficient heater premises. You just need to pay for the power consumed by the motor 200 W, and will go to the kitchen in 10 times great energy, 90 % which is pumped from the refrigerator chamber ( 90 % - Efficiency of the refrigerator in this example). It is curious that if instead of a refrigerator a heater of the same power was turned on, it would heat the room in 10 times weaker.

Our numerical estimates can be considered as an example of thermal environmental pollution characteristic of technical civilization.

Additional information

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm - J. de Boer Introduction to molecular physics and thermodynamics, Ed. IL, 1962 - pp. 202–205, part 2, ch. 2, § 10: the Claude-Heylandt gas liquefaction process is described.

Second law of thermodynamics: It is impossible to build a periodically operating heat engine that would convert all the heat supplied to it into work, i.e. Always .

French engineer Sadi Carnot proposed an ideal cycle that gives maximum efficiency. This cycle consists of two isotherms and two adiabats and is called Carnot cycle.

- isothermal expansion at , - adiabatic expansion , - isothermal compression at , - adiabatic compression .

Rice. 2.2 Carnot cycle in coordinates (P, V).

Let us calculate the efficiency of the Carnot cycle for an ideal gas. In an isothermal process, the internal energy of an ideal gas remains constant. Therefore, the amount of heat received by the gas is equal to the work done by the gas during the transition from state 1 to state 2 (Fig. 2.2). This work is equal to where is the mass of an ideal gas in a heat engine.

The amount of heat given off to the refrigerator is equal to the work expended on compressing the gas during its transition from state 3 to state 4. This work is equal to .

In order for the cycle to be closed, the state 1 And 4 must lie on the same adiabat. This implies the following condition:

Similarly for states 2 And 3 the following condition holds:

Dividing one ratio by the other, we arrive at cycle closure condition:

Substituting and into the expression for efficiency, we get:

. (2.2)

As a result, we obtain the formula for the efficiency of the Carnot cycle:

where is the temperature of the heater, is the temperature of the refrigerator. The efficiency of the Carnot cycle is the maximum efficiency of all possible cycles carried out in the given temperature intervals and.

Relation (2.2) is the content Carnot's theorem for a reversible cycle:

For irreversible cycle Carnot's theorem takes the form:

In general, you can combine these two records Carnot's theorem:

. (2.3)

Let us transform (2.3) as follows:

As a result we get

For a reversible Carnot cycle: ,

for an irreversible Carnot cycle: .

Then in the case of an arbitrary reversible cycle one can obtain:

and in the case of an arbitrary irreversible cycle:

Relation (2.4) shows that the quantity under the integral sign is a function of the state. This state function is designated by the letter S and is called entropy. Along with internal energy U entropy S plays an important role in thermodynamics.

End of work -

This topic belongs to the section:

Basic principles of molecular kinetic theory. Mass and size of molecules

Mkt studies the properties of a substance, pressure, temperature, and so on, as the total result of the actions of molecules, while using static...

If you need additional material on this topic, or you did not find what you were looking for, we recommend using the search in our database of works:

What will we do with the received material:

If this material was useful to you, you can save it to your page on social networks:

All topics in this section:

Basic principles of molecular kinetic theory
1. All substances consist of tiny particles - atoms and molecules. 2. Molecules and atoms of any substance are in continuous chaotic motion, which is called thermal motion

Mass and size of molecules
To characterize the masses of atoms and molecules, the following quantities are used: Atomic mass – the mass of an atom of a substance, expressed in amu. Molecular mass - mass

Thermodynamic parameters and processes. Equation of ideal gas
To describe the state of a thermodynamic system, physical quantities are introduced, which are called thermodynamic parameters or parameters of the state of the system. Usually as thermodyne

The main level of the molecular kinetic theory of eider
1) Gas molecules move only along three mutually perpendicular directions. If a vessel contains N molecules, then at any moment of time along each of the coordinate axes will move

The law of uniform distribution of energy across degrees of freedom. Internal energy of IS
The number of degrees of freedom i of a system is the number of independent quantities with which the position of the system can be specified. Thus, the position in space of a material point is completely

Maxwellian energy distribution over the degrees of freedom of gas molecules. Internal energy of an ideal gas
In the case of an ideal gas, the number of molecules per unit volume with velocity components in the range from vx to vx + dvx can be represented by

Characteristic velocities of gas molecules. Stern experience
1.-most probable speed of molecules

Boltzmann distribution of gas particles by potential energy. Maxwell-Boltzmann distribution
If the gas is in an external force field, then the gas particles have potential energy eп. Height distribution of ideal gas molecules in a uniform gravitational field.

Average free path of gas molecules. Concept of vacuum
The mean free path is the average distance traveled by a molecule between two successive collisions. On average, a molecule travels a distance per second

Transport phenomenon: thermal conductivity IG
Transport phenomena in gases. General patterns. The randomness of the thermal movement of gas molecules and continuous collisions between them lead to constant mixing of particles and changes in

Diffusion and internal friction in an ideal gas
The phenomenon of transfer - diffusion - consists of spontaneous mutual penetration and mixing of particles of two contacting gases, liquids and even solids. In this case, self-diffusion is distinguished

The first law of thermodynamics. Heat capacity of IG. Work of a gas when its volume changes
The first law of thermodynamics: The amount of heat imparted to a gas is used to increase the internal energy of the gas and to perform work on external bodies by the gas.

Thermodynamics of an isochoric process: V=const
Let's consider the law that describes this process and its graph in coordinates (P,V). This law is a special case of the Mendeleev-Clapeyron equation (the ideal gas equation of state)

Thermodynamics of an isothermal process: T=const
Let us present the law describing this process and its graph in coordinates (P,V). Having considered two states of an ideal gas 1 and 2, we obtain

Thermodynamics of the adiabatic process: dQ=0
An adiabatic process is a process that occurs without heat exchange with the environment. Since dQ = 0, the first law of thermodynamics takes the form:

Polytropic processes
Polytropic processes are processes in which the heat capacity of a gas remains constant. Let us find the equation of state of an ideal gas during a polytropic process, i.e. equation

Entropy and the 2nd law of thermodynamics
Entropy is a state function whose differential is determined by the relation:

Real gas. Van der Waals equation and its analysis. Critical state and its parameters
A real gas is a gas that is not described by the Clapeyron-Mendeleev equation of state for an ideal gas. The dependencies between its parameters show that molecules in a real gas interact

Lecture 13.

Heat and refrigeration machines. Second law of thermodynamics. Carnot cycle. Carnot's theorem. Thermodynamic temperature scale. Clausius inequality. Thermodynamic entropy. Law of increasing entropy. Third law of thermodynamics.

Thermal machines or heat engines , are designed to obtain useful work due to heat released as a result of chemical reactions (fuel combustion), nuclear transformations or for other reasons. For the operation of a heat engine, the following components are required: heater, refrigerator and working fluid .

The cooler can be, for example, the environment.

In what follows the concept will be used thermostat , by which we mean a body that is at a constant temperature and has an infinite heat capacity - any processes of receiving or releasing heat do not change the temperature of this body.

Cyclic (circular) thermodynamic process.

R Let's consider a cyclic process in which the heater transfers heat to the working fluid Q N. The working fluid does work and then gives off heat to the refrigerator Q X .

Comment. The presence of a stroke means. that the absolute value of the specified quantity is taken, i.e. Q X =  Q X  .

This circular process is called direct . In the direct process, heat is taken from a more heated body and after the system performs work on external bodies, the remainder of the heat is given to the less heated body. Heat engines operate in a direct cycle.

The process in which heat is taken from a less heated body and given to a more heated body as a result of work done on the system by external bodies is called reverse Refrigerators operate in a reverse cycle .

The heat received by the system is considered positive Q N > 0 , and the given one is negative Q X < 0 . If Q X > 0 – warmth, received refrigerator, then we can write:

Q X = Q X = Q X .

Internal energy is a function of state, therefore, during a circular (cyclic) process, when the system returns to its original state, the internal energy does not change. From the first law of thermodynamics it follows:

But since
, That

because
,
.

Direct cycle efficiency (thermal efficiency):

determined for cyclic (repeated) processes. (For non-cyclical process this kind of attitude is called useful way out.)

Comment. Heat transfer to the refrigerator is mandatory for the cyclic process. Otherwise, the working fluid will come into thermal equilibrium with the heater, and heat transfer from the heater will be impossible. Therefore, the efficiency of any heat engine is always less than unity:

In a refrigeration machine, external bodies do work A external by heat removal Q 2 from the cooled body and heat transfer Q 1  thermal reservoir (usually the environment). The efficiency of a refrigeration machine or refrigeration coefficient is the ratio of the amount of heat supplied to the work expended:

Generally speaking, this coefficient can be either less than unity or greater than one - it all depends on the work of external bodies.

Heat pump - a device that “pumps” heat from cold bodies to heated ones and is intended, for example, for heating a room. At the same time, the warmth is taken from the environment, which has a lower temperature, and heat is given to the air in the room . The heat pump operates in a reverse thermal cycle. (This heating principle is called dynamic heating). The efficiency of a heat pump is equal to the ratio of the heat transferred to the room to the work expended:

Since the heat removed from the environment is greater than zero, the efficiency of the heat pump is greater than one. But for the efficiency of the same direct cycle
,
, That's why