Teoria inegalităților trigonometrice. Inegalități trigonometrice simple și complexe

METODE DE REZOLVARE A INEGALĂȚILOR TRIGONOMETRICE

Relevanţă. Din punct de vedere istoric, ecuațiilor și inegalităților trigonometrice li s-a acordat un loc special în programa școlară. Putem spune că trigonometria este una dintre cele mai importante secțiuni ale cursului școlar și ale întregii științe matematice în general.

Ecuațiile și inegalitățile trigonometrice ocupă unul dintre locurile centrale în cursul de matematică din gimnaziu, atât în ​​ceea ce privește conținutul materialului educațional, cât și metodele de activitate educațională și cognitivă care pot și trebuie formate în cursul studiului lor și aplicate la rezolvarea unui număr mare. a problemelor de natură teoretică şi aplicativă .

Rezolvarea ecuațiilor trigonometrice și a inegalităților creează premisele pentru sistematizarea cunoștințelor elevilor legate de tot material educaționalîn trigonometrie (de exemplu, proprietăți ale funcțiilor trigonometrice, metode de transformare a expresiilor trigonometrice etc.) și face posibilă stabilirea de legături eficiente cu materialul studiat în algebră (ecuații, echivalență de ecuații, inegalități, transformări identice ale expresiilor algebrice etc. .).

Cu alte cuvinte, luarea în considerare a tehnicilor de rezolvare a ecuațiilor trigonometrice și a inegalităților implică un fel de transfer al acestor abilități către conținut nou.

Semnificația teoriei și numeroasele ei aplicații sunt o dovadă a relevanței temei alese. Aceasta, la rândul său, vă permite să determinați scopurile, obiectivele și subiectul cercetării lucrării cursului.

Scopul studiului: generalizează tipurile disponibile de inegalități trigonometrice, metode de bază și speciale de rezolvare a acestora, selectează un set de probleme pentru rezolvarea inegalităților trigonometrice de către școlari.

Obiectivele cercetării:

1. Pe baza unei analize a literaturii disponibile pe tema de cercetare, sistematizați materialul.

2. Furnizați un set de sarcini necesare pentru a consolida subiectul „Inegalități trigonometrice”.

Obiect de studiu sunt inegalități trigonometriceîntr-un curs școlar de matematică.

Subiect de studiu: tipuri de inegalități trigonometrice și metode de rezolvare a acestora.

Semnificație teoretică este de a sistematiza materialul.

Semnificație practică: aplicarea cunoștințe teoreticeîn rezolvarea problemelor; analiza principalelor metode comune de rezolvare a inegalităţilor trigonometrice.

Metode de cercetare : analiză literatura stiintifica, sinteza și generalizarea cunoștințelor dobândite, analiza soluțiilor sarcinilor, căutarea metode optime soluții la inegalități.

§1. Tipuri de inegalități trigonometrice și metode de bază de rezolvare a acestora

1.1. Cele mai simple inegalități trigonometrice

Două expresii trigonometrice legate prin semn sau > se numesc inegalități trigonometrice.

Rezolvarea unei inegalități trigonometrice înseamnă găsirea mulțimii de valori ale necunoscutelor incluse în inegalitatea pentru care inegalitatea este satisfăcută.

Partea principală a inegalităților trigonometrice este rezolvată prin reducerea lor la cea mai simplă soluție:

Aceasta poate fi o metodă de factorizare, schimbare a variabilei (
,
etc.), unde se rezolvă mai întâi inegalitatea obișnuită și apoi o inegalitate de formă
etc., sau alte metode.

Cele mai simple inegalități pot fi rezolvate în două moduri: folosind cercul unitar sau grafic.

Lăsaf(x  – una dintre funcțiile trigonometrice de bază. Pentru a rezolva inegalitatea
este suficient să-și găsești soluția pe o singură perioadă, adică. pe orice segment a cărui lungime este egală cu perioada funcțieif  X  . Apoi se va găsi soluția la inegalitatea inițialăX , precum și acele valori care diferă de cele găsite de orice număr întreg de perioade ale funcției. În acest caz, este convenabil să folosiți metoda grafică.

Să dăm un exemplu de algoritm pentru rezolvarea inegalităților
(
) Și
.

Algoritm pentru rezolvarea inegalității
(
).

1. Formulați definiția sinusului unui numărX pe cercul unitar.

3. Pe axa ordonatelor, marcați punctul cu coordonateleA .

4. Desenați o linie paralelă cu axa OX prin acest punct și marcați punctele sale de intersecție cu cerc.

5. Selectați un arc de cerc, toate punctele căruia au o ordonată mai mică decâtA .

6. Indicați direcția rundei (în sens invers acelor de ceasornic) și notați răspunsul adăugând perioada funcției la capetele intervalului2πn ,
.

Algoritm pentru rezolvarea inegalității
.

1. Formulați definiția tangentei unui numărX pe cercul unitar.

2. Desenați un cerc unitar.

3. Desenați o linie de tangente și marcați un punct cu o ordonată pe eaA .

4. Conectați acest punct cu originea și marcați punctul de intersecție al segmentului rezultat cu cercul unitar.

5. Selectați un arc de cerc, toate punctele căruia au o ordonată pe linia tangentă mai mică decâtA .

6. Indicați direcția parcurgerii și scrieți răspunsul ținând cont de domeniul de definire al funcției, adăugând un punctπn ,
(numărul din stânga în intrare este întotdeauna număr mai mic, stând în dreapta).

Interpretarea grafică a soluțiilor la ecuații simple și a formulelor de rezolvare a inegalităților în vedere generala sunt indicate în anexă (Anexele 1 și 2).

Exemplul 1. Rezolvați inegalitatea
.

Desenați o linie dreaptă pe cercul unității
, care intersectează cercul în punctele A și B.

Toate semnificațiiley pe intervalul NM este mai mare , toate punctele arcului AMB satisfac această inegalitate. La toate unghiurile de rotație, mare , dar mai mic ,
va prelua valori mai mari (dar nu mai mult de unul).

Fig.1

Astfel, soluția inegalității vor fi toate valorile din interval
, adică
. Pentru a obține toate soluțiile acestei inegalități, este suficient să adăugați la capetele acestui interval
, Unde
, adică
,
. Rețineți că valorile
Și
sunt rădăcinile ecuației
,

acestea.
;
.

Răspuns:
,
.

1.2. Metoda grafica

În practică, metoda grafică de rezolvare a inegalităților trigonometrice se dovedește adesea a fi utilă. Să luăm în considerare esența metodei folosind exemplul inegalității
:

1. Dacă argumentul este complex (diferit deX ), apoi înlocuiți-l cut .

2. Construim într-una plan de coordonate jucărie grafice de funcții
Și
.

3. Găsim astfeldouă puncte de intersecție adiacente ale graficelor, între careundă sinusoidalăsituatsuperior Drept
. Găsim abscisele acestor puncte.

4. Scrieți o inegalitate dublă pentru argumentt , ținând cont de perioada cosinus (t va fi între abscisele găsite).

5. Faceți o înlocuire inversă (reveniți la argumentul inițial) și exprimați valoareaX din dubla inegalitate scriem raspunsul sub forma unui interval numeric.

Exemplul 2. Rezolvați inegalitatea: .

La rezolvarea inegalităților folosind metoda grafică, este necesar să se construiască grafice ale funcțiilor cât mai precis posibil. Să transformăm inegalitatea în forma:

Să construim grafice ale funcțiilor într-un sistem de coordonate
Și
(Fig. 2).

Fig.2

Graficele funcțiilor se intersectează în punctA cu coordonate
;
. Intre
puncte grafice
sub punctele graficului
. Și atunci când
valorile funcției sunt aceleași. De aceea
la
.

Răspuns:
.

1.3. Metoda algebrică

Destul de des, inegalitatea trigonometrică originală poate fi redusă la o inegalitate algebrică (rațională sau irațională) printr-o substituție bine aleasă. Această metodă presupune transformarea unei inegalități, introducerea unei substituții sau înlocuirea unei variabile.

Să ne uităm la exemple concrete aplicarea acestei metode.

Exemplul 3. Reducere la forma cea mai simplă
.

(Fig. 3)

Fig.3

,
.

Răspuns:
,

Exemplul 4. Rezolvați inegalitatea:

ODZ:
,
.

Folosind formule:
,

Să scriem inegalitatea sub forma:
.

Sau, crezând
după simple transformări obținem

,

,

.

Rezolvând ultima inegalitate folosind metoda intervalului, obținem:

Fig.4

, respectiv
. Apoi din Fig. 4 urmează
, Unde
.

Fig.5

Răspuns:
,
.

1.4. Metoda intervalului

Schema generală de rezolvare a inegalităților trigonometrice folosind metoda intervalului:

Prin utilizarea formule trigonometrice factorizați.

Găsiți punctele de discontinuitate și zerourile funcției și plasați-le pe cerc.

Luați orice punctLA (dar nu a fost găsit mai devreme) și află semnul produsului. Dacă produsul este pozitiv, atunci plasați un punct în afara cercului unitar pe raza corespunzătoare unghiului. În caz contrar, plasați punctul în interiorul cercului.

Dacă punctul se întâlnește număr par ori, să-l numim un punct de multiplicitate par dacă este un număr impar de ori, îl vom numi un punct de multiplicitate impar. Desenați arce după cum urmează: începeți dintr-un punctLA , dacă următorul punct este de multiplicitate impară, atunci arcul intersectează cercul în acest punct, dar dacă punctul este de multiplicitate pară, atunci nu se intersectează.

Arcurile din spatele cercului sunt intervale pozitive; în interiorul cercului există spații negative.

Exemplul 5. Rezolvați inegalitatea

,
.

Puncte din prima serie:
.

Puncte din a doua serie:
.

Fiecare punct apare de un număr impar de ori, adică toate punctele sunt de multiplicitate impară.

Să aflăm semnul produsului la
: . Să marchem toate punctele de pe cercul unitar (Fig. 6):

Orez. 6

Răspuns:
,
;
,
;
,
.

Exemplul 6 . Rezolvați inegalitatea.

Soluţie:

Să găsim zerourile expresiei .

A primiaem :

,
;

,
;

,
;

,
;

Pe valorile seriei cercului unitarX 1 reprezentate prin puncte
. SerieX 2 dă puncte
. O serieX 3 obținem două puncte
. În sfârșit, serialulX 4 va reprezenta puncte
. Să reprezentăm toate aceste puncte pe cercul unitar, indicând multiplicitatea acestuia în paranteze lângă fiecare dintre ele.

Lasă acum numărul va fi egal. Să facem o estimare pe baza semnului:

Deci, punctA trebuie selectat pe raza care formează unghiul cu grindăOh, în afara cercului unitar. (Rețineți că fasciculul auxiliarDESPRE A Nu este deloc necesar să o înfățișați într-o imagine. PunctA este ales aproximativ.)

Acum din punct de vedereA trageți o linie continuă ondulată succesiv la toate punctele marcate. Și la puncte
linia noastră merge dintr-o zonă în alta: dacă era în afara cercului unității, atunci merge în interiorul acestuia. Apropiindu-se de punct , linia revine în regiunea interioară, deoarece multiplicitatea acestui punct este pară. În mod similar la punct (cu multiplicitate egală) linia trebuie îndreptată către regiunea exterioară. Deci, am desenat o anumită imagine prezentată în Fig. 7. Ajută la evidențierea zonelor dorite de pe cercul unității. Sunt marcate cu semnul „+”.

Fig.7

Răspuns final:

Notă. Dacă o linie ondulată, după ce a ocolit toate punctele marcate pe cercul unității, nu poate fi returnată la punctA , fără a traversa cercul într-un loc „ilegal”, aceasta înseamnă că a fost făcută o eroare în soluție, și anume, un număr impar de rădăcini a fost ratat.

Răspuns: .

§2. Un set de probleme pentru rezolvarea inegalităților trigonometrice

În procesul de dezvoltare a capacității școlarilor de a rezolva inegalitățile trigonometrice, se pot distinge și 3 etape.

1. pregătitoare,

2. dezvoltarea capacităţii de rezolvare a inegalităţilor trigonometrice simple;

3. introducerea inegalităţilor trigonometrice de alte tipuri.

Scopul etapei pregătitoare este acela că este necesar să se dezvolte la școlari capacitatea de a utiliza un cerc sau un grafic trigonometric pentru a rezolva inegalitățile, și anume:

Capacitatea de a rezolva inegalități simple ale formei
,
,
,
, utilizarea proprietăților funcțiilor sinus și cosinus;

Capacitatea de a construi inegalități duble pentru arce de cerc numeric sau pentru arce de grafice ale funcțiilor;

Capacitatea de a efectua diverse transformări ale expresiilor trigonometrice.

Se recomandă implementarea acestei etape în procesul de sistematizare a cunoștințelor școlarilor despre proprietățile funcțiilor trigonometrice. Principalele mijloace pot fi sarcinile oferite elevilor și efectuate fie sub îndrumarea unui profesor, fie independent, precum și abilitățile dezvoltate în rezolvarea ecuațiilor trigonometrice.

Iată exemple de astfel de sarcini:

1 . Marcați un punct pe cercul unității , Dacă

.

2. În ce sfert din planul de coordonate este situat punctul? , Dacă este egal cu:

3. Marcați punctele pe cercul trigonometric , Dacă:

4. Convertiți expresia în funcții trigonometriceeusferturi.

A)
, b)
, V)

5. Arc MR este dat.M - mijloceu- al treilea trimestru,R - mijlocIItrimestrul. Limitați valoarea unei variabilet pentru: (faceți o inegalitate dublă) a) arc MR; b) arcele RM.

6. Notați inegalitatea dublă pentru secțiunile selectate ale graficului:

Orez. 1

7. Rezolvați inegalitățile
,
,
,
.

8. Conversia expresiei .

La a doua etapă a învăţării rezolvării inegalităţilor trigonometrice, putem oferi următoarele recomandări legate de metodologia de organizare a activităţilor elevilor. În acest caz, este necesar să ne concentrăm pe abilitățile existente ale elevilor în lucrul cu un cerc sau grafic trigonometric, format în timpul rezolvării celor mai simple ecuații trigonometrice.

În primul rând, se poate motiva oportunitatea obținerii unei metode generale de rezolvare a celor mai simple inegalități trigonometrice, apelând, de exemplu, la o inegalitate de formă
. Folosind cunoștințele și abilitățile dobândite în etapa pregătitoare, elevii vor aduce în formă inegalitatea propusă
, dar poate fi dificil să găsească un set de soluții la inegalitatea rezultată, deoarece Este imposibil să o rezolvi doar folosind proprietățile funcției sinus. Această dificultate poate fi evitată apelând la ilustrația corespunzătoare (rezolvarea grafică a ecuației sau folosind un cerc unitar).

În al doilea rând, profesorul ar trebui să atragă atenția elevilor asupra diferite căi finalizați sarcina, oferiți un exemplu adecvat de rezolvare a inegalității atât grafic, cât și folosind un cerc trigonometric.

Să luăm în considerare următoarele soluții ale inegalității
.

1. Rezolvarea inegalității folosind cercul unitar.

În prima lecție de rezolvare a inegalităților trigonometrice, vom oferi studenților un algoritm de rezolvare detaliat, care într-o prezentare pas cu pas reflectă toate abilitățile de bază necesare rezolvării inegalității.

Pasul 1.Să desenăm un cerc unitar și să marchem un punct pe axa ordonatelor și trageți o linie dreaptă prin ea paralelă cu axa x. Această linie va intersecta cercul unitar în două puncte. Fiecare dintre aceste puncte reprezintă numere al căror sinus este egal cu .

Pasul 2.Această linie dreaptă a împărțit cercul în două arce. Să-l selectăm pe cel care prezintă numere care au un sinus mai mare decât . Desigur, acest arc este situat deasupra liniei drepte trasate.

Orez. 2

Pasul 3.Selectați unul dintre capetele arcului marcat. Să notăm unul dintre numerele care este reprezentat de acest punct al cercului unitar .

Pasul 4.Pentru a selecta numărul corespunzător celui de-al doilea capăt al arcului selectat, „mergem” de-a lungul acestui arc de la capătul numit la celălalt. În același timp, amintiți-vă că atunci când vă deplasăm în sens invers acelor de ceasornic, numerele prin care vom trece cresc (când ne deplasăm în sens opus, numerele ar scădea). Să notăm numărul care este reprezentat pe cercul unității de al doilea capăt al arcului marcat .

Astfel, vedem acea inegalitate
satisface numerele pentru care inegalitatea este adevărată
. Am rezolvat inegalitatea pentru numerele situate pe aceeași perioadă a funcției sinus. Prin urmare, toate soluțiile inegalității pot fi scrise sub forma

Elevii ar trebui să fie rugați să examineze cu atenție desenul și să descopere de ce toate soluțiile la inegalitate
poate fi scris sub forma
,
.

Orez. 3

Este necesar să atragem atenția elevilor asupra faptului că atunci când rezolvăm inegalități pentru funcția cosinus, trasăm o dreaptă paralelă cu axa ordonatelor.

Metoda grafică de rezolvare a inegalităților.

Construim grafice
Și
, dat fiind
.

Orez. 4

Apoi scriem ecuația
si decizia lui
,
,
, găsit folosind formule
,
,
.

(Dăruindn valorile 0, 1, 2, găsim cele trei rădăcini ale ecuației compilate). Valori
sunt trei abscise consecutive ale punctelor de intersecție ale graficelor
Și
. Evident, mereu la interval
inegalitatea este valabilă
, iar pe interval
– inegalitatea
. Ne interesează primul caz, iar apoi adăugând la capetele acestui interval un număr care este un multiplu al perioadei sinusului, obținem o soluție a inegalității.
la fel de:
,
.

Orez. 5

Rezuma. Pentru a rezolva inegalitatea
, trebuie să creați ecuația corespunzătoare și să o rezolvați. Găsiți rădăcinile din formula rezultată Și , și scrieți răspunsul la inegalitate sub forma: ,
.

În al treilea rând, faptul despre mulțimea de rădăcini a inegalității trigonometrice corespunzătoare este confirmat foarte clar atunci când o rezolvăm grafic.

Orez. 6

Este necesar să le demonstrăm elevilor că turnul, care este soluția inegalității, se repetă în același interval, egal cu perioada funcției trigonometrice. De asemenea, puteți lua în considerare o ilustrație similară pentru graficul funcției sinus.

În al patrulea rând, este recomandabil să se efectueze lucrări de actualizare a tehnicilor elevilor pentru conversia sumei (diferențelor) funcțiilor trigonometrice într-un produs și să se atragă atenția elevilor asupra rolului acestor tehnici în rezolvarea inegalităților trigonometrice.

O astfel de muncă poate fi organizată prin îndeplinirea independentă de către elevi a sarcinilor propuse de profesor, dintre care evidențiem următoarele:

În al cincilea rând, elevilor trebuie să li se ceară să ilustreze soluția fiecărei inegalități trigonometrice simple folosind un grafic sau un cerc trigonometric. Cu siguranță ar trebui să acordați atenție oportunității sale, în special utilizării cercului, deoarece atunci când rezolvați inegalitățile trigonometrice, ilustrația corespunzătoare servește ca un mijloc foarte convenabil de înregistrare a setului de soluții la o anumită inegalitate.

Se recomandă introducerea elevilor în metode de rezolvare a inegalităților trigonometrice care nu sunt cele mai simple după următoarea schemă: trecerea la o anumită inegalitate trigonometrică trecerea la ecuația trigonometrică corespunzătoare căutarea comună (profesor - elevi) pentru o soluție transfer independent al metoda găsită la alte inegalități de același tip.

Pentru a sistematiza cunoștințele elevilor despre trigonometrie, recomandăm selectarea specială a unor astfel de inegalități, a căror rezolvare necesită diverse transformări care pot fi implementate în procesul de rezolvare a acesteia și focalizarea atenției elevilor asupra trăsăturilor lor.

Ca atare inegalități productive putem propune, de exemplu, următoarele:

În concluzie, dăm un exemplu de set de probleme pentru rezolvarea inegalităților trigonometrice.

1. Rezolvați inegalitățile:

2. Rezolvați inegalitățile: 3. Găsiți toate soluțiile la inegalități: 4. Găsiți toate soluțiile la inegalități:

A)
, îndeplinind condiția
;

b)
, îndeplinind condiția
.

5. Găsiți toate soluțiile la inegalități:

A) ;

b) ;

V)
;

G)
;

d)
.

6. Rezolvați inegalitățile:

A) ;

b) ;

V) ;

G)
;

d) ;

e) ;

și)
.

7. Rezolvați inegalitățile:

A)
;

b) ;

V) ;

G).

8. Rezolvați inegalitățile:

A) ;

b) ;

V) ;

G)
;

d)
;

e) ;

și)
;

h) .

Este recomandabil să oferiți sarcinile 6 și 7 studenților care studiază matematica la nivel ridicat, sarcina 8 – pentru elevii claselor cu studii avansate de matematică.

§3. Metode speciale soluții la inegalitățile trigonometrice

Metode speciale pentru rezolvarea ecuațiilor trigonometrice - adică acele metode care pot fi folosite doar pentru rezolvarea ecuațiilor trigonometrice. Aceste metode se bazează pe utilizarea proprietăților funcțiilor trigonometrice, precum și pe utilizarea diferitelor formule și identități trigonometrice.

3.1. Metoda sectorială

Să luăm în considerare metoda sectorială pentru rezolvarea inegalităților trigonometrice. Rezolvarea inegalităților de formă

, UndeP ( X ) ȘiQ ( X ) – rațional funcții trigonometrice(sinusurile, cosinusurile, tangentele și cotangentele sunt incluse în ele rațional), similar cu rezolvarea inegalităților raționale. Este convenabil să se rezolve inegalitățile raționale folosind metoda intervalelor pe dreapta numerică. Analogul său pentru rezolvarea inegalităților trigonometrice raționale este metoda sectoarelor din cercul trigonometric, pt.sinx Șicosx (
) sau semicerc trigonometric pentrutgx Șictgx (
).

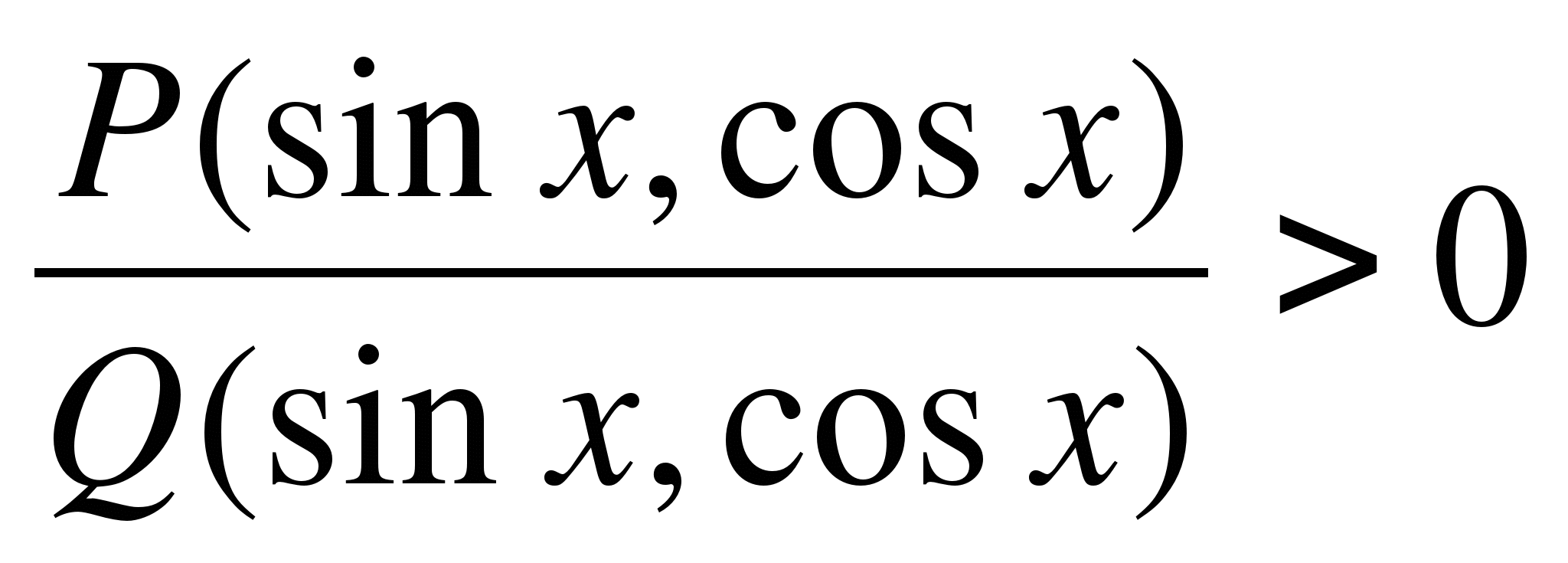
În metoda intervalului, fiecare factor liniar al numărătorului și numitorului formei
pe axa numerelor corespunde unui punct , iar la trecerea prin acest punct
schimba semnul. În metoda sectorului, fiecare factor al formei
, Unde
- una dintre funcțiisinx saucosx Și
, într-un cerc trigonometric îi corespund două unghiuri Și
, care împart cercul în două sectoare. La trecere prin Și funcţie
schimba semnul.

Trebuie reținut următoarele:

a) Factorii formei
Și
, Unde
, păstrați semnul pentru toate valorile . Astfel de factori ai numărătorului și numitorului sunt eliminați prin schimbare (dacă
) cu fiecare astfel de respingere, semnul de inegalitate este inversat.

b) Factorii formei
Și
sunt de asemenea aruncate. Mai mult, dacă aceștia sunt factori ai numitorului, atunci inegalitățile de formă sunt adăugate sistemului echivalent de inegalități
Și
. Dacă aceștia sunt factori ai numărătorului, atunci în sistemul echivalent de restricții corespund inegalităților
Și
în cazul unei inegalități inițiale stricte și egalitate
Și
în cazul unei inegalităţi iniţiale nestricte. La aruncarea multiplicatorului
sau
semnul inegalității este inversat.

Exemplul 1. Rezolvați inegalitățile: a)
, b)
. avem funcția b) . Rezolvați inegalitatea pe care o avem,

3.2. Metoda cercului concentric

Această metodă este un analog al metodei axelor numerice paralele pentru rezolvarea sistemelor de inegalități raționale.

Să luăm în considerare un exemplu de sistem de inegalități.

Exemplul 5. Rezolvați un sistem de inegalități trigonometrice simple

În primul rând, rezolvăm fiecare inegalitate separat (Figura 5). În colțul din dreapta sus al figurii vom indica pentru ce argument se ia în considerare cercul trigonometric.

Fig.5

Apoi, construim un sistem de cercuri concentrice pentru argumentX . Desenăm un cerc și îl umbrim conform soluției primei inegalități, apoi desenăm un cerc de rază mai mare și îl umbrim conform soluției celei de-a doua, apoi construim un cerc pentru a treia inegalitate și un cerc de bază. Desenăm raze din centrul sistemului prin capetele arcelor, astfel încât acestea să intersecteze toate cercurile. Formăm o soluție pe cercul de bază (Figura 6).

Fig.6

Răspuns:
,
.

Concluzie

Toate sarcinile cercetarea cursului au fost finalizate. Materialul teoretic este sistematizat: sunt date principalele tipuri de inegalități trigonometrice și principalele metode de rezolvare a acestora (grafică, algebrică, metoda intervalelor, sectoarelor și metoda cercurilor concentrice). Pentru fiecare metodă a fost dat un exemplu de rezolvare a unei inegalități. Partea teoretică a fost urmată de partea practică. Conține un set de sarcini pentru rezolvarea inegalităților trigonometrice.

Acest curs poate fi folosit de studenți pentru muncă independentă. Elevii pot verifica nivelul de stăpânire a acestui subiect și pot exersa îndeplinirea sarcinilor de complexitate diferită.

După ce am studiat literatura relevantă despre această problemăÎn mod evident, putem concluziona că abilitatea și abilitățile de a rezolva inegalitățile trigonometrice în cursul școlar de algebră și începuturile de analiză sunt foarte importante, a căror dezvoltare necesită un efort semnificativ din partea profesorului de matematică.

De aceea acest lucru va fi util pentru profesorii de matematică, deoarece face posibilă organizarea eficientă a pregătirii elevilor pe tema „Inegalități trigonometrice”.

Cercetarea poate fi continuată prin extinderea acesteia la o lucrare finală de calificare.

Lista literaturii folosite

Bogomolov, N.V. Culegere de probleme de matematică [Text] / N.V. Bogomolov. – M.: Butarda, 2009. – 206 p.

Vygodsky, M.Ya. Manual de matematică elementară [Text] / M.Ya. Vygodski. – M.: Butarda, 2006. – 509 p.

Zhurbenko, L.N. Matematică în exemple și probleme [Text] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 p.

Ivanov, O.A. Matematică elementară pentru școlari, elevi și profesori [Text] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 p.

Karp, A.P. Teme de algebră și începuturi de analiză pentru organizarea repetiției finale și certificarea în clasa a 11-a [Text] / A.P. Crap. – M.: Educație, 2005. – 79 p.

Kulanin, E.D. 3000 de probleme de concurs la matematică [Text] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 p.

Leibson, K.L. Colectie sarcini practiceîn matematică [Text] / K.L. Leibson. – M.: Butarda, 2010. – 182 p.

Cot, V.V. Probleme cu parametrii și soluția acestora. Trigonometrie: ecuații, inegalități, sisteme. clasa a X-a [Text] / V.V. Cot. – M.: ARKTI, 2008. – 64 p.

Manova, A.N. Matematică. Tutor expres pentru pregătirea pentru examenul de stat unificat: student. manual [Text] / A.N. Manova. – Rostov-pe-Don: Phoenix, 2012. – 541 p.

Mordkovich, A.G. Algebra și începuturile analiză matematică. 10-11 clase. Manual pentru elevi institutii de invatamant[Text] / A.G. Mordkovici. – M.: Iris-press, 2009. – 201 p.

Novikov, A.I. Funcții trigonometrice, ecuații și inegalități [Text] / A.I. Novikov. – M.: FIZMATLIT, 2010. – 260 p.

Oganesyan, V.A. Metode de predare a matematicii în liceu: Tehnica generala. Manual manual pentru studenții la fizică - mat. fals. ped. Inst. [Text] / V.A. Oganesyan. – M.: Educație, 2006. – 368 p.

Olehnik, S.N. Ecuații și inegalități. Metode non-standard hotărâri [Text] / S.N. Olehnik. – M.: Editura Factorial, 1997. – 219 p.

Sevriukov, P.F. Trigonometric, exponențial și ecuații logaritmiceși inegalități [Text] / P.F. Sevriukov. – M.: Educație publică, 2008. – 352 p.

Sergheev, I.N. Examen de stat unificat: 1000 de probleme cu răspunsuri și soluții la matematică. Toate sarcinile grupei C [Text] / I.N. Sergheev. – M.: Examen, 2012. – 301 p.

Sobolev, A.B. Matematică elementară [Text] / A.B. Sobolev. – Ekaterinburg: Instituția de Învățământ de Stat de Învățământ Profesional Superior USTU-UPI, 2005. – 81 p.

Fenko, L.M. Metoda intervalelor în rezolvarea inegalităților și studierea funcțiilor [Text] / L.M. Fenko. – M.: Butarda, 2005. – 124 p.

Friedman, L.M. Baza teoretica metode de predare a matematicii [Text] / L.M. Friedman. – M.: Casa de carte „LIBROKOM”, 2009. – 248 p.

Anexa 1

Interpretarea grafică a soluțiilor la inegalități simple

Orez. 1

Orez. 2

Fig.3

Fig.4

Fig.5

Fig.6

Fig.7

Fig.8

Anexa 2

Soluții la inegalități simple

La rezolvarea inegalităților care conțin funcții trigonometrice, acestea se reduc la cele mai simple inegalități de forma cos(t)>a, sint(t)=a și altele similare. Și deja cele mai simple inegalități sunt rezolvate. Să ne uităm la diverse exemple modalități de rezolvare a inegalităților trigonometrice simple.

Exemplul 1. Rezolvați inegalitatea sin(t) > = -1/2.

Desenați un cerc unitar. Deoarece sin(t) prin definiție este coordonata y, se marchează punctul y = -1/2 pe axa Oy. Tragem o linie dreaptă prin ea paralelă cu axa Ox. La intersecția dreptei cu graficul cercului unitar, marcați punctele Pt1 și Pt2. Conectăm originea coordonatelor cu punctele Pt1 și Pt2 prin două segmente.

Soluția acestei inegalități vor fi toate punctele cercului unitar situat deasupra acestor puncte. Cu alte cuvinte, soluția va fi arcul l. Acum este necesar să indicați condițiile în care un punct arbitrar va aparține arcului l.

Pt1 se află în semicercul drept, ordonata sa este -1/2, apoi t1=arcsin(-1/2) = - pi/6. Pentru a descrie punctul Pt1, puteți scrie următoarea formulă:
t2 = pi - arcsin(-1/2) = 7*pi/6. Ca rezultat, obținem următoarea inegalitate pentru t:

Păstrăm inegalitățile. Și deoarece funcția sinus este periodică, înseamnă că soluțiile se vor repeta la fiecare 2*pi. Adăugăm această condiție la inegalitatea rezultată pentru t și notăm răspunsul.

Raspuns: -pi/6+2*pi*n< = t < = 7*pi/6 + 2*pi*n, при любом целом n.

Exemplul 2. Rezolvați inegalitatea cos(t).<1/2.

Să desenăm un cerc unitar. Deoarece, conform definiției, cos(t) este coordonata x, marchem punctul x = 1/2 pe grafic pe axa Ox.
Tragem o linie dreaptă prin acest punct paralelă cu axa Oy. La intersecția dreptei cu graficul cercului unitar, marcați punctele Pt1 și Pt2. Conectăm originea coordonatelor cu punctele Pt1 și Pt2 prin două segmente.

Soluțiile vor fi toate punctele cercului unitar care aparțin arcului l Să găsim punctele t1 și t2.

t1 = arccos(1/2) = pi/3.

t2 = 2*pi - arccos(1/2) = 2*pi-pi/3 = 5*pi/6.

Am obținut inegalitatea pentru t: pi/3

Deoarece cosinusul este o funcție periodică, soluțiile se vor repeta la fiecare 2*pi. Adăugăm această condiție la inegalitatea rezultată pentru t și notăm răspunsul.

Răspuns: pi/3+2*pi*n

Exemplul 3. Rezolvați inegalitatea tg(t)< = 1.

Perioada tangentei este egală cu pi. Să găsim soluții care aparțin intervalului (-pi/2;pi/2) semicerc drept. Apoi, folosind periodicitatea tangentei, notăm toate soluțiile acestei inegalități. Să desenăm un cerc unitar și să marchem o linie de tangente pe el.

Dacă t este o soluție a inegalității, atunci ordonata punctului T = tg(t) trebuie să fie mai mică sau egală cu 1. Mulțimea acestor puncte va alcătui raza AT. Mulțimea punctelor Pt care va corespunde punctelor acestei raze este arcul l. Mai mult, punctul P(-pi/2) nu aparține acestui arc.

În timpul lecției practice, vom repeta principalele tipuri de sarcini din tema „Trigonometrie”, vom analiza suplimentar probleme de complexitate crescută și vom lua în considerare exemple de rezolvare a diferitelor inegalități trigonometrice și sistemele acestora.

Această lecție vă va ajuta să vă pregătiți pentru unul dintre tipurile de sarcini B5, B7, C1 și C3.

Să începem prin a trece în revistă principalele tipuri de sarcini pe care le-am abordat în subiectul „Trigonometrie” și să rezolvăm mai multe probleme non-standard.

Sarcina nr. 1. Convertiți unghiurile în radiani și grade: a) ; b) .

a) Să folosim formula pentru conversia gradelor în radiani

Să înlocuim valoarea specificată în ea.

b) Aplicați formula de conversie a radianilor în grade

Să efectuăm înlocuirea .

Răspuns. A) ; b) .

Sarcina nr. 2. Calculați: a) ; b) .

a) Deoarece unghiul depășește cu mult tabelul, îl vom reduce scăzând perioada sinusului. Deoarece Unghiul este indicat în radiani, atunci vom considera perioada ca .

b) În acest caz situația este similară. Deoarece unghiul este indicat în grade, vom considera perioada tangentei ca .

Unghiul rezultat, deși mai mic decât perioada, este mai mare, ceea ce înseamnă că nu se mai referă la partea principală, ci la partea extinsă a mesei. Pentru a nu vă antrena din nou memoria memorând tabelul extins al valorilor trigofuncțiilor, să scădem din nou perioada tangentei:

Am profitat de ciudățenia funcției tangente.

Răspuns. a) 1; b) .

Sarcina nr. 3. calculati , Dacă .

Să reducem întreaga expresie la tangente împărțind numărătorul și numitorul fracției la . În același timp, nu ne putem teme de asta, pentru că în acest caz, valoarea tangentei nu ar exista.

Sarcina nr. 4. Simplificați expresia.

Expresiile specificate sunt convertite folosind formule de reducere. Sunt scrise în mod neobișnuit folosind grade. Prima expresie reprezintă în general un număr. Să simplificăm toate trigofuncțiile una câte una:

Deoarece , apoi funcția se schimbă într-o cofuncție, adică. la cotangentă, iar unghiul se încadrează în al doilea sfert, în care tangenta inițială are semn negativ.

Din aceleași motive ca și în expresia anterioară, funcția se schimbă într-o cofuncție, i.e. la cotangentă, iar unghiul se încadrează în primul sfert, în care tangenta inițială are semn pozitiv.

Să înlocuim totul într-o expresie simplificată:

Problema #5. Simplificați expresia.

Să scriem tangenta unghiului dublu folosind formula corespunzătoare și să simplificăm expresia:

Ultima identitate este una dintre formulele universale de înlocuire a cosinusului.

Problema #6. Calculati.

Principalul lucru este să nu faci greșeala standard și să nu dai răspunsul că expresia este egală cu . Nu puteți folosi proprietatea de bază a arctangentei atâta timp cât există un factor sub formă de doi lângă el. Pentru a scăpa de ea, vom scrie expresia conform formulei pentru tangentei unui unghi dublu, tratând , ca pe un argument obișnuit.

Acum putem aplica proprietatea de bază a arctangentei, amintiți-vă că nu există restricții asupra rezultatului său numeric.

Problema nr. 7. Rezolvați ecuația.

Când se rezolvă o ecuație fracțională care este egală cu zero, se indică întotdeauna că numărătorul este egal cu zero, dar numitorul nu este, deoarece Nu poți împărți la zero.

Prima ecuație este un caz special al celei mai simple ecuații care poate fi rezolvată folosind un cerc trigonometric. Amintiți-vă singuri această soluție. A doua inegalitate este rezolvată ca cea mai simplă ecuație folosind formula generală pentru rădăcinile tangentei, dar numai cu semnul diferit.

După cum vedem, o familie de rădăcini exclude o altă familie de exact același tip de rădăcini care nu satisfac ecuația. Acestea. fara radacini.

Răspuns. Nu există rădăcini.

Problema nr. 8. Rezolvați ecuația.

Să observăm imediat că putem elimina factorul comun și să o facem:

Ecuația a fost redusă la una dintre formele standard, în care produsul mai multor factori este egal cu zero. Știm deja că, în acest caz, fie unul dintre ele este egal cu zero, fie celălalt, fie al treilea. Să scriem asta sub forma unui set de ecuații:

Primele două ecuații sunt cazuri speciale ale celor mai simple, am întâlnit deja de multe ori ecuații similare, așa că le vom indica imediat soluțiile. Reducem a treia ecuație la o funcție folosind formula sinusului cu unghi dublu.

Să rezolvăm ultima ecuație separat:

Această ecuație nu are rădăcini, deoarece valoarea sinusului nu poate depăși .

Astfel, soluția este doar primele două familii de rădăcini, acestea pot fi combinate într-una, ceea ce este ușor de arătat pe cercul trigonometric:

Aceasta este o familie cu toate jumătățile, adică

Să trecem la rezolvarea inegalităților trigonometrice. În primul rând, vom analiza abordarea rezolvării exemplului fără a folosi formule pentru soluții generale, ci folosind cercul trigonometric.

Problema nr. 9. Rezolvați inegalitatea.

Să desenăm o linie auxiliară pe cercul trigonometric corespunzătoare unei valori sinus egale cu , și să arătăm intervalul de unghiuri care satisfac inegalitatea.

Este foarte important să înțelegeți exact cum să indicați intervalul rezultat al unghiurilor, de ex. care este începutul și care este sfârșitul lui. Începutul intervalului va fi unghiul corespunzător punctului în care vom intra chiar la începutul intervalului dacă ne mișcăm în sens invers acelor de ceasornic. În cazul nostru, acesta este punctul care se află în stânga, pentru că deplasându-ne în sens invers acelor de ceasornic și trecând de punctul potrivit, noi, dimpotrivă, părăsim intervalul necesar de unghiuri. Punctul potrivit va corespunde, prin urmare, sfârșitului decalajului.

Acum trebuie să înțelegem unghiurile începutului și sfârșitului intervalului nostru de soluții la inegalitate. O greșeală tipică este să indicați imediat că punctul din dreapta corespunde unghiului, cel din stânga și să dați răspunsul. Nu este adevarat! Vă rugăm să rețineți că tocmai am indicat intervalul corespunzător părții superioare a cercului, deși ne interesează partea inferioară, cu alte cuvinte, am amestecat începutul și sfârșitul intervalului de soluție de care avem nevoie.

Pentru ca intervalul să înceapă din colțul punctului drept și să se termine cu colțul punctului din stânga, este necesar ca primul unghi specificat să fie mai mic decât al doilea. Pentru a face acest lucru, va trebui să măsurăm unghiul punctului drept în direcția negativă de referință, adică. în sensul acelor de ceasornic și va fi egal cu . Apoi, începând să ne mișcăm din el în sensul acelor de ceasornic pozitiv, vom ajunge la punctul din dreapta după punctul din stânga și vom obține valoarea unghiului pentru acesta. Acum începutul intervalului de unghiuri este mai mic decât sfârșitul și putem scrie intervalul de soluții fără a lua în considerare perioada:

Având în vedere că astfel de intervale se vor repeta de un număr infinit de ori după orice număr întreg de rotații, obținem o soluție generală ținând cont de perioada sinusului:

Punem paranteze pentru că inegalitatea este strictă și alegem punctele de pe cerc care corespund capetelor intervalului.

Comparați răspunsul primit cu formula pentru soluția generală pe care am dat-o în prelegere.

Răspuns. .

Această metodă este bună pentru a înțelege de unde provin formulele pentru soluțiile generale ale celor mai simple inegalități trigon. În plus, este util celor care sunt prea leneși să învețe toate aceste formule greoaie. Cu toate acestea, metoda în sine nu este ușoară, alegeți care abordare a soluției este cea mai convenabilă pentru dvs.

Pentru a rezolva inegalitățile trigonometrice, puteți utiliza și grafice ale funcțiilor pe care este construită o linie auxiliară, similar cu metoda prezentată folosind un cerc unitar. Dacă sunteți interesat, încercați să vă dați seama singuri această abordare a soluției. În cele ce urmează vom folosi formule generale pentru a rezolva inegalitățile trigonometrice simple.

Problema nr. 10. Rezolvați inegalitatea.

Să folosim formula pentru soluția generală, ținând cont de faptul că inegalitatea nu este strictă:

În cazul nostru obținem:

Răspuns.

Problema nr. 11. Rezolvați inegalitatea.

Să folosim formula generală a soluției pentru inegalitatea strictă corespunzătoare:

Răspuns. .

Problema nr. 12. Rezolvați inegalități: a) ; b) .

În aceste inegalități, nu este nevoie să vă grăbiți să folosiți formule pentru soluții generale sau cercul trigonometric, este suficient să vă amintiți pur și simplu intervalul de valori sinus și cosinus.

a) Din moment ce , atunci inegalitatea nu are sens. Prin urmare, nu există soluții.

b) Pentru că în mod similar, sinusul oricărui argument satisface întotdeauna inegalitatea specificată în condiție. Prin urmare, inegalitatea este satisfăcută de toate valorile reale ale argumentului.

Răspuns. a) nu există soluții; b) .

Problema 13. Rezolvați inegalitatea .

Cele mai simple inegalități trigonometrice de forma sin x>a stau la baza rezolvării inegalităților trigonometrice mai complexe.

Să luăm în considerare rezolvarea celor mai simple inegalități trigonometrice de forma sin x>a pe cercul unitar.

1) la 0

Folosind asocierea cosinus-bun (ambele încep cu co-, ambele sunt „rotunde”), ne amintim că cosinus este x, respectiv sinus este y. De aici construim un grafic y=a - o linie dreaptă paralelă cu axa bou. Dacă inegalitatea este strictă, punctele de intersecție ale cercului unitar și dreapta y=a sunt perforate, dacă inegalitatea nu este strictă, pictăm peste puncte (cât de ușor este să ne amintim când este perforat un punct și când este umbrită, vezi). Cea mai mare dificultate în rezolvarea celor mai simple inegalități trigonometrice este cauzată de găsirea corectă a punctelor de intersecție a cercului unitar și a dreptei y=a.

Primul punct este ușor de găsit - este arcsin a. Stabilim calea pe care mergem de la primul punct la al doilea. Pe linia y=a sinx=a, deasupra, deasupra liniei, sin x>a, iar dedesubt, sub linie, sin x a, avem nevoie de calea de sus. Astfel, de la primul punct, arcsin a, până la al doilea, mergem în sens invers acelor de ceasornic, adică în direcția de creștere a unghiului. Nu ajungem la punct. Cât ne lipsește? Pe arcsin a. Deoarece nu am ajuns la n, atunci al doilea punct este mai mic decât n, ceea ce înseamnă că pentru a-l găsi, trebuie să scădem arcsina din n. Soluția inegalității sin x>a în acest caz este intervalul de la arcsin a la n-arcsin a. Deoarece perioada sinusului este 2n, pentru a lua în considerare toate soluțiile inegalității (și există un număr infinit de astfel de intervale), adăugăm 2n la fiecare capăt al intervalului, unde n este un număr întreg (n aparține la Z).

2) a=0, adică sin x>0

În acest caz, primul punct al intervalului este 0, al doilea este n La ambele capete ale intervalului, ținând cont de perioada sinusului, adăugăm 2n.

3) pentru a=-1, adică sinx>-1

În acest caz, primul punct este p/2, iar pentru a ajunge la al doilea, ocolim întregul cerc în sens invers acelor de ceasornic. Ajungem la punctul -p/2+2p=3p/2. Pentru a lua în considerare toate intervalele care sunt soluții la această inegalitate, adăugăm 2n la ambele capete.

4) sinx>-a, la 0

Primul punct este, ca de obicei, arcsin(-a)=-arcsina. Pentru a ajunge la al doilea punct, mergem pe calea superioară, adică în direcția de creștere a unghiului.

De data aceasta trecem dincolo de n. Cât mai mergem? Pe arcsin x. Aceasta înseamnă că al doilea punct este n+arcsin x. De ce nu există minus? Pentru că minusul din notația -arcsin a înseamnă mișcare în sensul acelor de ceasornic, dar am mers în sens invers acelor de ceasornic. Și, în final, adăugați 2pn la fiecare capăt al intervalului.

5) sinx>a, dacă a>1.

Cercul unitar se află în întregime sub linia dreaptă y=a. Nu există niciun punct deasupra liniei drepte. Deci nu există soluții.

6) sinx>-a, unde a>1.

În acest caz, întregul cerc unitar se află în întregime deasupra liniei drepte y=a. Prin urmare, orice punct satisface condiția sinx>a. Aceasta înseamnă că x este orice număr.

Și aici x este orice număr, deoarece punctele -n/2+2nn sunt incluse în soluție, în contrast cu inegalitatea strictă sinx>-1. Nu este nevoie să excludeți nimic.

Singurul punct de pe cerc care satisface această condiție este n/2. Ținând cont de perioada sinusului, soluția acestei inegalități este mulțimea punctelor x=n/2+2n.

De exemplu, rezolvați inegalitatea sinx>-1/2: