Задача 1. Игрок записывал выигрыш знаком + и проигрыш знаком –. Найти результат каждой из следующих записей: a) +7 руб. +4 руб.; b) –3 руб. –6 руб.; c) –4 р. +4 р.; d) +8 р. –6 р.; e) –11 р. +7 р.; f) +2 р. +3 р. –5 р.; g) +6 р. –4 р. +3 р. –5 р. +2 р. –6 р.
Запись a) указывает, что игрок сначала выиграл 7 руб. и затем еще выиграл 4 р., – итого выиграл 11 р.; запись c) указывает, что сначала игрок проиграл 4 р. и затем выиграл 4 р., – потому общий результат = 0 (игрок ничего не сделал); запись e) указывает, что игрок сначала проиграл 11 руб., потом выиграл 7 руб., – проигрыш пересиливает выигрыш на 4 руб.; следовательно, в общем, игрок проиграл 4 руб. Итак, имеем право для этих записей записать, что
a) +7 р. +4 р. = +11 р.; c) –4 р. +4 р. = 0; e) –11 р. + 7 р. = –4 руб.
Так же легко разбираются и остальные записи.
По своему смыслу эти задачи сходны с теми, которые в арифметике решаются с помощью действия сложения, поэтому и здесь мы станем считать, что везде приходится для нахождения общего результата игры складывать относительные числа, выражающие результаты отдельных игр, например, в примере c) относительное число –11 руб. складывается с относительным числом +7 руб.
Задача 2. Кассир записывал приход кассы знаком +, а расход знаком –. Найти общий результат каждой из следующих записей: a) +16 р. +24 р.; b) –17 р. –48 р.; c) +26 р. –26 р.; d) –24 р. +56 р.; e) –24 р. +6 р.; f) –3 р. +25 р. –20 р. +35 р.; g) +17 р. –11 р. +14 р. –9 р. –18 р. +7 р.; h) –9 р –7 р. +15 р. –11 р. +4 р.
Разберем, напр., запись f): сосчитаем сперва весь приход кассы: по этой записи было 25 руб. приходу, да еще 35 руб. приходи, итого приходу было 60 руб., а расходу было 3 руб., да еще 20 руб., итого было 23 руб. расходу; приход превышает расход на 37 руб. След.,
– 3 руб. + 25 руб. – 20 руб. + 35 руб. = +37 руб.
Задача 3. Точка колеблется по прямой, начиная от точки A (черт. 2).
Черт. 2.
Перемещение ее вправо обозначаем знаком + и перемещение ее влево знаком –. Где будет находиться точка после нескольких колебаний, записанных одною из следующих записей: a) +2 дм. –3 дм. +4 дм.; b) –1 дм. +2 дм. +3 дм. +4 дм. –5 дм. +3 дм.; c) +10 дм. –1 дм. +8 дм. –2 дм. +6 дм. –3 дм. +4 дм. –5 дм.; d) –4 дм. +1 дм. –6 дм. +3 дм. –8 дм. +5 дм.; e) +5 дм. –6 дм. +8 дм. –11 дм. На чертеже дюймы обозначены отрезками, меньшими настоящих.
Последнюю запись (e) разберем: сначала колеблющаяся точка передвинулась вправо от A на 5 дм., потом передвинулась влево на 6 дм., – в общем, она должна оказаться находящеюся влево от A на 1 дм., потом подвинулась вправо на 8 дюйм., след., теперь она находится вправо от A на 7 дм., а затем подвинулась влево на 11 дм., следовательно, она находится влево от A на 4 дм.
Остальные примеры предоставляем разобрать самим учащимся.
Мы приняли, что во всех разобранных записях приходится складывать записанные относительные числа. Поэтому условимся:
Если несколько относительных чисел написаны рядом (с их знаками), то эти числа надо сложить.
Разберем теперь главные случаи, встречающиеся при сложении, причем возьмем относительные числа без названий (т. е. вместо того, чтобы говорить, напр., 5 руб. выигрышу, да еще 3 руб. проигрышу, или точка переместилась на 5 дм. вправо от A, да потом еще на 3 дм. Влево, станем говорить 5 положительных единиц, да еще 3 отрицательных единиц …).
Здесь надо сложить числа, состоящие из 8 полож. единиц, да еще из 5 полож. единиц, получим число, состоящее из 13 полож. единиц.
Итак, + 8 + 5 = 13
Здесь надо сложить число, состоящее из 6 отрицат. единиц с числом, состоящим из 9 отрицат. единиц, получим 15 отрицат. единиц (сравнить: 6 рублей проигрыша и 9 руб. проигрыша – составят 15 руб. проигрыша). Итак,
– 6 – 9 = – 15.
4 рубля выигрыша да затем 4 руб. проигрыша, в общем, дадут нуль (взаимно уничтожается); также, если точка продвинулась от A сначала вправо на 4 дм., а потом влево на 4 дм., то она окажется опять в точке A и, след., окончательное ее расстояние от A равно нулю, и вообще мы должны считать, что 4 полож. единицы, да еще 4 отрицательных единицы, в общем, дадут нуль, или взаимно уничтожатся. Итак,
4 – 4 = 0, также – 6 + 6 = 0 и т. д.
Два относительных числа, имеющие одинаковую абсолютную величину, но различные знаки, взаимно уничтожаются.
6 отрицат. единиц уничтожатся с 6 положит. единицами, да еще останется 3 полож. единицы. Итак,
– 6 + 9 = + 3.
7 полож. единиц уничтожатся с 7 отрицат. единицами, да еще останется 4 отрицат. единицы. Итак,
7 – 11 = – 4.
Рассматривая 1), 2), 4) и 5) случаи, имеем
8 + 5 = + 13; – 6 – 9 = – 15; – 6 + 9 = + 3 и
+ 7 – 11 = – 4.
Отсюда видим, что надо различать два случая сложения алгебраических чисел: случай, когда слагаемые имеют одинаковые знаки (1-й и 2-й) и случай сложения чисел с разными знаками (4-й и 5-й).
Не трудно теперь увидать, что
при сложении чисел с одинаковыми знаками следует сложить их абсолютные величины и написать их общий знак, а при сложении двух чисел с разными знаками надо вычесть арифметически их абсолютные величины (из большей меньшую) и написать знак того числа, у которого абсолютная величина больше.
Пусть требуется найти сумму
6 – 7 – 3 + 5 – 4 – 8 + 7 + 9.
Мы можем сначала сложить все положительные числа + 6 + 5 + 7 + 9 = + 27, потом все отрицат. – 7 – 3 – 4 – 8 = – 22 и затем полученные результаты между собою + 27 – 22 = + 5.
Можем также воспользоваться здесь тем, что числа + 5 – 4 – 8 + 7 взаимно уничтожаются и тогда остается сложить лишь числа + 6 – 7 – 3 + 9 = + 5.
Другой способ обозначения сложения
Можно каждое слагаемое заключать в скобки и между скобками написать знак сложения. Напр.:
(+7) + (+9); (–3) + (–8); (+7) + (–11); (–4) + (+5);
(–3) + (+5) + (–7) + (+9) + (–11) и т. п.
Мы можем, согласно предыдущему, сразу написать сумму, напр. (–4) + (+5) = +1 (случай сложения чисел с разными знаками: надо из большей абсолютной величины вычесть меньшую и написать знак того числа, у которого абсолютная величина больше), но можем также переписать сначала то же самое без скобок, пользуясь нашим условием, что если числа написаны рядом с их знаками, то эти числа надо сложить; след.,
чтобы раскрыть скобки при сложении положительных и отрицательных чисел, надо слагаемые написать рядом с их знаками (знак сложения и скобки опустить).
Напр.: (+ 7) + (+ 9) = + 7 + 9; (– 3) + (– 8) = – 3 – 8; (+ 7) + (– 11) = + 7 – 11; (– 4) + (+ 5) = – 4 + 5; (– 3) + (+ 5) + (– 7) + (+ 9) + (– 11) = – 3 + 5 – 7 + 9 – 11.
После этого можно полученные числа сложить.
В курсе алгебры следует обратить особенное внимание на уменье раскрывать скобки.
Упражнения.
1) (– 7) + (+ 11) + (– 15) + (+ 8) + (– 1);
>>Математика: Сложение чисел с разными знаками
33. Сложение чисел с разными знаками
Если температура воздуха была равна 9 °С, а потом она изменилась на - 6 °С (т. е. понизилась на 6 °С), то она стала равной 9 + (- 6) градусам (рис. 83).
Чтобы сложить числа 9 и - 6 с помощью , надо точку А (9) переместить влево на 6 единичных отрезков (рис. 84). Получим точку В (3).
Значит, 9+(- 6) = 3. Число 3 имеет тот же знак, что и слагаемое 9, а его модуль равен разности модулей слагаемых 9 и -6.
Действительно, |3| =3 и |9| - |- 6| = = 9 - 6 = 3.
Если та же температура воздуха 9 °С изменилась на -12 °С (т. е. понизилась на 12 °С), то она стала равной 9 +(-12) градусам (рис. 85). Сложив числа 9 и -12 с помощью координатной прямой (рис. 86), получим 9 + (-12)= -3. Число -3 имеет тот же знак, что и слагаемое -12, а его модуль равен разности модулей слагаемых -12 и 9.
Действительно, | - 3| = 3 и | -12| - | -9| =12 - 9 = 3.
Чтобы сложить два числа с разными знаками, надо:
1) из большего модуля слагаемых вычесть меньший;
2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
Обычно сначала определяют и записывают знак суммы, а потом находят разность модулей.

Например:
1) 6,1+(- 4,2)= +(6,1 - 4,2)= 1,9,
или короче 6,1+(- 4,2) = 6,1 - 4,2 = 1,9;

При сложении положительных и отрицательных чисел можно использовать микрокалькулятор . Чтобы ввести отрицательное число в микрокалькулятор, надо ввести модуль этого числа, потом нажать клавишу «изменение знака» |/-/|. Например, чтобы ввести число -56,81, надо последовательно нажимать клавиши: | 5 |, | 6 |, | ¦ |, | 8 |, | 1 |, |/-/|. Операции над числами любого знака выполняются на микрокалькуляторе так же, как над положительными числами.
Например, сумму -6,1 + 3,8 вычисляют по Программе
? Числа а и b имеют разные знаки. Какой знак будет иметь сумма этих чисел, если больший модуль имеет отрицательное число?
если меньший модуль имеет отрицательное число?
если больший модуль имеет положительное число?
если меньший модуль имеет положительное число?
Сформулируйте правило сложения чисел с разными знаками. Как ввести в микрокалькулятор отрицательное число?
К 1045. Число 6 изменили на -10. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 6 и -10?
1046. Число 10 изменили на -6. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма 10 и -6?
1047. Число -10 изменили на 3. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма -10 и 3?
1048. Число -10 изменили на 15. С какой стороны от начала отсчета расположено получившееся число? На каком расстоянии от начала отсчета оно находится? Чему равна сумма -10 и 15?
1049. В первую половину дня температура изменилась на - 4 °С, а во вторую - на + 12 °С. На сколько градусов изменилась температура в течение дня?
1050. Выполните сложение:

1051. Прибавьте:
а) к сумме -6 и -12 число 20;
б) к числу 2,6 сумму -1,8 и 5,2;
в) к сумме -10 и -1,3 сумму 5 и 8,7;
г) к сумме 11 и -6,5 сумму -3,2 и -6.
1052. Какое из чисел 8; 7,1; -7,1; -7; -0,5 является корнем уравнения - 6 + х =-13,1?
1053. Угадайте корень уравнения и выполните проверку:
а) х + (-3)= -11; в) m + (-12) = 2;
б) - 5 + y=15; г) 3 + n = -10.
1054. Найдите значение выражения:
1055. Выполните действия с помощью микрокалькулятора:
а) - 3,2579 + (-12,308); г) -3,8564+ (-0,8397) +7,84;
б) 7,8547+ (- 9,239); д) -0,083 + (-6,378) + 3,9834;
в) -0,00154 + 0,0837; е) -0,0085+ 0,00354+ (- 0,00921).
П 1056. Найдите значение суммы:

1057. Найдите значение выражения:
1058. Сколько целых чисел расположено между числами:
а) 0 и 24; б) -12 и -3; в) -20 и 7?
1059. Представьте число -10 в виде суммы двух отрицательных слагаемых так, чтобы:
а) оба слагаемых были целыми числами;
б) оба слагаемых были десятичными дробями;
в) одно из слагаемых было правильной обыкновенной дробью
.
1060. Каково расстояние (в единичных отрезках) между точками координатной прямой с координатами:
а) 0 и а; б) -а и а; в) -а и 0; г) а и -За?
М 1061. Радиусы географических параллелей земной поверхности, на которых расположены города Афины и Москва, соответственно равны 5040 км и 3580 км (рис. 87). На сколько параллель Москвы короче параллели Афин?

1062. Составьте уравнение для решения задачи: «Поле площадью 2,4 га разделили на два участка. Найдите площадь каждого участка, если известно, что один из участков:
а) на 0,8 га больше другого;
б) на 0,2 га меньше другого;
в) в 3 раза больше другого;
г) в 1,5 раза меньше другого;
д) составляет другого;
е) составляет 0,2 другого;
ж) составляет 60% другого;
з) составляет 140% другого».
1063. Решите задачу:
1) В первый день путешественники проехали 240 км, во второй день 140 км, в третий день они проехали в 3 раза больше, чем во второй, а в четвертый день они отдыхали. Сколько километров они проехали в пятый день, если за 5 дней они проезжали в среднем по 230 км в день?
2) Заработок отца в месяц равен 280 р. Стипендия дочери в 4 раза меньше. Сколько зарабатывает в месяц мать, если в семье 4 человека, младший сын - школьник и на каждого приходится в среднем 135 р.?
1064. Выполните действия:
1) (2,35 + 4,65) 5,3:(40-2,9);
2) (7,63-5,13) 0,4:(3,17 + 6,83).

1066. Представьте в виде суммы двух равных слагаемых кдое из чисел:
1067. Найдите значение а + b, если:
а) а= -1,6, b = 3,2; б) а=- 2,6, b = 1,9; в)![]()
1068. На одном этаже жилого дома было 8 квартир. 2 квартиры имели жилую площадь по 22,8 м 2 , 3 квартиры - по 16,2 м 2 , 2 квартиры - по 34 м 2 . Какую жилую площадь имела восьмая квартира, если на этом этаже в среднем на каждую квартиру приходилось по 24,7 м 2 жилой площади?
1069.В составе товарного поезда было 42 вагона. Крытых вагонов было в 1,2 раза больше, чем платформ, а число цистерн составляло числа платформ. Сколько вагонов каждого вида было в составе поезда?
1070. Найдите значение выражения
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Планирование по математике, учебники и книги онлайн , курсы и задачи по математике для 6 класса скачать
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиНа действиях с положительными и отрицательными числами основан практически весь курс математики. Ведь как только мы приступаем к изучению координатной прямой, числа со знаками «плюс» и «минус» начинают встречаться нам повсеместно, в каждой новой теме. Нет ничего проще, чем сложить между собой обычные положительные числа, нетрудно и вычесть одно из другого. Даже арифметические действия с двумя отрицательными числами редко становятся проблемой.
Однако многие путаются в сложении и вычитании чисел с разными знаками. Напомним правила, по которым происходят эти действия.
Сложение чисел с разными знаками
Если для решения задачи нам требуется прибавить к некоторому числу «а» отрицательное число «-b», то действовать нужно следующим образом.
- Возьмем модули обоих чисел - |a| и |b| - и сравним эти абсолютные значения между собой.
- Отметим, какой из модулей больше, а какой меньше, и вычтем из большего значения меньшее.
- Поставим перед получившимся числом знак того числа, модуль которого больше.
Это и будет ответом. Можно выразиться проще: если в выражении a + (-b) модуль числа «b» больше, чем модуль «а», то мы отнимаем «а» из «b» и ставим «минус» перед результатом. Если больше модуль «а», то «b» вычитается из «а» - а решение получается со знаком «плюс».
Бывает и так, что модули оказываются равны. Если так, то на этом месте можно остановиться - речь идет о противоположных числах, и их сумма всегда будет равна нулю.
Вычитание чисел с разными знаками
Со сложением мы разобрались, теперь рассмотрим правило для вычитания. Оно тоже довольно простое - и кроме того, полностью повторяет аналогичное правило для вычитания двух отрицательных чисел.
Для того, чтобы вычесть из некоего числа «а» - произвольного, то есть с любым знаком - отрицательное число «с», нужно прибавить к нашему произвольному числу «а» число, противоположное «с». Например:
- Если «а» - положительное число, а «с» - отрицательное, и из «а» нужно вычесть «с», то записываем так: а – (-с) = а + с.
- Если «а» - отрицательное число, а «с» - положительное, и из «а» нужно вычесть «с», то записываем следующим образом: (- а)– с = - а+ (-с).
Таким образом, при вычитании чисел с разными знаками в итоге мы возвращаемся к правилам сложения, а при сложении чисел с разными знаками - к правилам вычитания. Запоминание данных правил позволяет решать задачи быстро и без труда.
На этом уроке мы узнаем, что такое отрицательное число и какие числа называются противоположными. Также научимся складывать отрицательные и положительные числа (числа с разными знаками) и разберём несколько примеров сложения чисел с разными знаками.
Посмотрите на эту шестеренку (см. рис. 1).
Рис. 1. Шестеренка часов
Это не стрелка, которая непосредственно показывает время и не циферблат (см. рис. 2). Но без этой детали часы не работают.

Рис. 2. Шестеренка внутри часов
А что обозначает буква Ы? Ничего, кроме звука Ы. Но без нее не будут «работать» многие слова. Например, слово «мЫшь». Так и отрицательные числа: они не показывают никакого количества, но без них механизм вычислений был бы существенно труднее.
Мы знаем, что сложение и вычитание равноправные операции, и их можно выполнять в любом порядке. В записи в прямом порядке мы можем посчитать: , а начать с вычитания нет, так как мы не договорились еще, а что же такое .
Понятно, что увеличить число на , а потом уменьшить на означает в итоге уменьшение на три. Почему бы так и не обозначить этот объект и так и считать: прибавить - значит вычесть . Тогда .
Число может означать, например, яблока. Новое число не обозначает никакого реального количества. Само по себе оно ничего не означает, как буква Ы. Это просто новый инструмент для упрощения вычислений.
Назовем новые числа отрицательными . Теперь мы можем вычитать из меньшего числа большее. Технически всё равно нужно вычесть из большего числа меньшего, но в ответе поставить знак минус: .
Рассмотрим ещё один пример: ![]() . Можно сделать все действия подряд: .
. Можно сделать все действия подряд: .
Однако из первого числа легче вычесть третье, а потом прибавить второе число:
Отрицательные числа можно определить и по-другому.
Для каждого натурального числа, например , введем новое число, которое обозначим , и определим, что оно обладает следующим свойством: сумма числа и равна : .
Число будем называть отрицательным, а числа и - противоположными. Таким образом, мы получили бесконечное количество новых чисел, например:
Противоположное для числа ;
Противоположное числу ;
Противоположное числу ; ![]()
Противоположное числу ;
Вычтем из меньшего числа большее: . Прибавим к данному выражению : . Получили ноль. Однако согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять : . Следовательно, выражение можно обозначить как .
У каждого положительного числа существует число-близнец, которое отличается только тем, что перед ним стоит знак минус Такие числа называются противоположными (см. рис. 3).

Рис. 3. Примеры противоположных чисел
Свойства противоположных чисел
1. Сумма противоположных чисел равна нулю: .
2. Если из нуля вычесть положительное число, то результатом будет противоположное отрицательное число: .
1. Оба числа могут быть положительными, и складывать их мы уже умеем: .
2. Оба числа могут быть отрицательными.
Мы уже прошли сложение таких чисел на предыдущем уроке, но убедимся, что понимаем, что с ними делать. Например: .
Чтобы эту сумму найти, складываем противоположные положительные числа и и ставим знак минус.
3. Одно число может быть положительным, а другое - отрицательным.
Прибавление отрицательного числа мы, если это нам удобно, можем заменять на вычитание положительного: .
Ещё один пример: . Опять сумму записываем как разность. Вычесть из меньшего большее число можно, вычитая из большего меньшее, но поставив знак минус.
Слагаемые можем менять местами: .
Ещё один аналогичный пример: .
Во всех случаях в итоге получается вычитание.
Чтобы коротко сформулировать эти правила, давайте вспомним еще один термин. Противоположные числа, конечно, не равны друг другу. Но было бы странно не заметить у них общего. Это общее мы назвали модулем числа . Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного - противоположному, положительному. Например: , .
Чтобы сложить два отрицательных числа, нужно сложить их модули и поставить знак минус:
Чтобы сложить отрицательное и положительное число, нужно из большего модуля вычесть меньший модуль и поставить знак числа с большим модулем:
Оба числа отрицательные, следовательно, складываем их модули и ставим знак минус:
Два числа с разными знаками, следовательно, из модуля числа (больший модуль) вычитаем модуль числа и ставим знак минус (знак числа с большим модулем):
Два числа с разными знаками, следовательно, из модуля числа (больший модуль) вычитаем модуль числа и ставим знак минус (знак числа с большим модулем): .
Два числа с разными знаками, следовательно, из модуля числа (больший модуль) вычитаем модуль числа и ставим знак плюс (знак числа с большим модулем): .
У положительных и отрицательных чисел исторически разная роль.
Сначала мы ввели натуральные числа для счета предметов:
Потом мы ввели другие положительные числа - дроби, для счета нецелых количеств, частей: .
Отрицательные же числа появились как инструмент для упрощения расчетов. Не было такого, чтобы в жизни были какие-то количества, которые нам было не посчитать, и мы изобрели отрицательные числа.
То есть отрицательные числа не возникли из реального мира. Просто они оказались настолько удобными, что кое-где им нашлось применение и в жизни. Например, мы часто слышим про отрицательную температуру. При этом мы никогда не сталкиваемся с отрицательным количеством яблок. В чем же разница?
Разница в том, что в жизни отрицательные величины используют только для сравнения, но не для количеств. Если в гостинице оборудовали подвал и туда пустили лифт, то, чтобы оставить привычную нумерацию обычных этажей, может появиться минус первый этаж. Этот минус первый означает всего лишь на этаж ниже уровня земли (см. рис. 1).

Рис. 4. Минус первый и минус второй этажи
Отрицательная температура отрицательна только по сравнению с нулем, который выбрал автор шкалы Андерс Цельсий. Есть другие шкалы, и та же самая температура уже может не быть там отрицательной.
При этом мы понимаем, что невозможно поменять точку отсчета так, чтобы яблок стало не пять, а шесть. Таким образом, в жизни положительные числа используются для определения количеств ( яблок, торта).
Еще мы их используем вместо имен. Каждому телефону можно было бы дать свое имя, но количество имен ограничено, а чисел нет. Поэтому мы используем номера для телефонов. Также для упорядочивания ( век идет за веком).
Отрицательные числа в жизни используются в последнем смысле (минус первый этаж ниже нулевого и первого этажей)
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. «Гимназия», 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6 классов заочной школы МИФИ. М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. М.: Просвещение, Библиотека учителя математики, 1989.
- Math-prosto.ru ().
- Youtube ().
- School-assistant.ru ().
- Allforchildren.ru ().
Домашнее задание
В этой статье мы разберемся со сложением чисел с разными знаками . Здесь мы приведем правило сложения положительного и отрицательного числа, и рассмотрим примеры применения этого правила при сложении чисел с разными знаками.
Навигация по странице.
Правило сложения чисел с разными знаками
Положительные и отрицательные числа можно трактовать как имущество и долг соответственно, при этом модули чисел показывают величину имущества и долга. Тогда сложение чисел с разными знаками можно рассматривать как сложение имущества и долга. При этом понятно, что если имущество меньше долга, то после взаимозачета останется долг, если имущество больше долга, то после взаимозачета останется имущество, а если имущество равно долгу, то после расчетов не останется ни долга, ни имущества.
Объединим приведенные выше рассуждения в правило сложения чисел с разными знаками . Чтобы сложить положительное и отрицательное число, надо:
- найти модули слагаемых;
- сравнить полученные числа, при этом
- если полученные числа равны, то исходные слагаемые являются противоположными числами, и их сумма равна нулю,
- если же полученные числа не равны, то надо запомнить знак числа, модуль которого больше;
- из большего модуля вычесть меньший;
- перед полученным числом поставить знак того слагаемого, модуль которого больше.
- Плюс на минус дает минус;
- Минус на минус дает плюс.
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Озвученное правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшего числа. Также понятно, что в результате сложения положительного и отрицательного числа может получиться или положительное число, или отрицательное число, или нуль.
Также заметим, что правило сложения чисел с разными знаками справедливо для целых чисел, для рациональных чисел и для действительных чисел.
Примеры сложения чисел с разными знаками
Рассмотрим примеры сложения чисел с разными знаками по правилу, разобранному в предыдущем пункте. Начнем с простого примера.
www.cleverstudents.ru
Сложение и вычитание дробей
Дроби - это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители - и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где - плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель - и наоборот. Ну и конечно, не забывайте два простых правила:
Разберем все это на конкретных примерах:
![]()
В первом случае все просто, а во втором внесем минусы в числители дробей:

Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
![]()
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.

Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей - это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните - обязательно повторите. Примеры:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:

Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры - и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
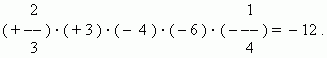











Вопрос: До завтра нужно срочно!
Стихотворение Ивана Бунина "Детство": анализ и история создания Школьный анализ стихотворения Бунина И
Произведения, заслуживающие звания "самая красивая картина в мире" Самые красивые картины известных художников
Красота и польза русской земли — луговые и полевые цветы
История и основные идеи декаданса как направления культуры и искусства Декаданс в искусстве