Résolution d'intégrales de fractions rationnelles. Intégration de fractions rationnelles

Le matériel présenté dans ce sujet est basé sur les informations présentées dans le sujet « Fractions rationnelles. Décomposition de fractions rationnelles en fractions élémentaires (simples) ». Je vous recommande fortement de parcourir au moins ce sujet avant de passer à la lecture de ce document. De plus, nous aurons besoin d'un tableau d'intégrales indéfinies.

Permettez-moi de vous rappeler quelques termes. Ils ont été abordés dans le sujet correspondant, je me limiterai donc ici à une brève formulation.

Le rapport de deux polynômes $\frac(P_n(x))(Q_m(x))$ est appelé fonction rationnelle ou fraction rationnelle. La fraction rationnelle s'appelle correct, si $n< m$, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если $n ≥ m$) дробь называется faux.

Les fractions rationnelles élémentaires (les plus simples) sont des fractions rationnelles de quatre types :

1. $\frac(A)(x-a)$ ;
2. $\frac(A)((x-a)^n)$ ($n=2,3,4, \ldots$);
3. $\frac(Mx+N)(x^2+px+q)$ ($p^2-4q< 0$);
4. $\frac(Mx+N)((x^2+px+q)^n)$ ($p^2-4q< 0$; $n=2,3,4,\ldots$).

Remarque (souhaitable pour une compréhension plus complète du texte) : afficher\masquer

Pourquoi la condition $p^2-4q est-elle nécessaire ?< 0$ в дробях третьего и четвертого типов? Рассмотрим квадратное уравнение $x^2+px+q=0$. Дискриминант этого уравнения $D=p^2-4q$. По сути, условие $p^2-4q < 0$ означает, что $D < 0$. Если $D < 0$, то уравнение $x^2+px+q=0$ не имеет действительных корней. Т.е. выражение $x^2+px+q$ неразложимо на множители. Именно эта неразложимость нас и интересует.

Par exemple, pour l'expression $x^2+5x+10$ on obtient : $p^2-4q=5^2-4\cdot 10=-15$. Puisque $p^2-4q=-15< 0$, то выражение $x^2+5x+10$ нельзя разложить на множители.

D'ailleurs, pour cette vérification il n'est pas du tout nécessaire que le coefficient avant $x^2$ soit égal à 1. Par exemple, pour $5x^2+7x-3=0$ on obtient : $D=7^ 2-4\cdot 5 \cdot (-3)=109$. Puisque $D > 0$, l'expression $5x^2+7x-3$ est factorisable.

Des exemples de fractions rationnelles (bonnes et impropres), ainsi que des exemples de décomposition d'une fraction rationnelle en fractions élémentaires peuvent être trouvés. Nous ne nous intéresserons ici qu'aux questions de leur intégration. Commençons par l'intégration des fractions élémentaires. Ainsi, chacun des quatre types de fractions élémentaires ci-dessus est facile à intégrer à l’aide des formules ci-dessous. Permettez-moi de vous rappeler que lors de l'intégration de fractions de types (2) et (4), $n=2,3,4,\ldots$ sont supposés. Les formules (3) et (4) nécessitent la réalisation de la condition $p^2-4q< 0$.

\begin(équation) \int \frac(A)(x-a) dx=A\cdot \ln |x-a|+C \end(equation) \begin(equation) \int\frac(A)((x-a)^n )dx=-\frac(A)((n-1)(x-a)^(n-1))+C \end(equation) \begin(equation) \int \frac(Mx+N)(x^2 +px+q) dx= \frac(M)(2)\cdot \ln (x^2+px+q)+\frac(2N-Mp)(\sqrt(4q-p^2))\arctg\ frac(2x+p)(\sqrt(4q-p^2))+C \end(équation)

Pour $\int\frac(Mx+N)((x^2+px+q)^n)dx$ la substitution $t=x+\frac(p)(2)$ est effectuée, après quoi l'intervalle résultant est Divisé en deux. Le premier sera calculé en entrant sous le signe différentiel, et le second aura la forme $I_n=\int\frac(dt)((t^2+a^2)^n)$. Cette intégrale est prise en utilisant la relation de récurrence

\begin(équation) I_(n+1)=\frac(1)(2na^2)\frac(t)((t^2+a^2)^n)+\frac(2n-1)(2na ^2)Je_n,\; n\in N\fin(équation)

Le calcul d'une telle intégrale est discuté dans l'exemple n°7 (voir la troisième partie).

Schéma de calcul des intégrales de fonctions rationnelles (fractions rationnelles) :

1. Si l'intégrande est élémentaire, appliquez les formules (1) à (4).
2. Si l'intégrande n'est pas élémentaire, représentez-le comme une somme de fractions élémentaires, puis intégrez à l'aide des formules (1) - (4).

L'algorithme ci-dessus pour intégrer des fractions rationnelles présente un avantage indéniable : il est universel. Ceux. en utilisant cet algorithme, vous pouvez intégrer n'importe lequel fraction rationnelle. C'est pourquoi presque tous les changements de variables dans une intégrale indéfinie (Euler, Chebyshev, substitution trigonométrique universelle) sont effectués de telle manière qu'après ce changement on obtient une fraction rationnelle sous l'intervalle. Et puis appliquez-lui l’algorithme. Nous analyserons l'application directe de cet algorithme à l'aide d'exemples, après avoir pris une petite note.

$$ \int\frac(7dx)(x+9)=7\ln|x+9|+C. $$

En principe, cette intégrale est facile à obtenir sans application mécanique de la formule. Si nous retirons la constante $7$ du signe intégral et prenons en compte que $dx=d(x+9)$, nous obtenons :

$$ \int\frac(7dx)(x+9)=7\cdot \int\frac(dx)(x+9)=7\cdot \int\frac(d(x+9))(x+9 )=|u=x+9|=7\cdot\int\frac(du)(u)=7\ln|u|+C=7\ln|x+9|+C. $$

Pour des informations détaillées, je vous recommande de consulter le sujet. Il explique en détail comment ces intégrales sont résolues. À propos, la formule est prouvée par les mêmes transformations qui ont été appliquées dans ce paragraphe lors de sa résolution « manuelle ».

2) Là encore, il existe deux manières : utiliser la formule toute faite ou s'en passer. Si vous appliquez la formule, vous devez alors tenir compte du fait que le coefficient devant $x$ (numéro 4) devra être supprimé. Pour ce faire, retirons simplement ces quatre éléments entre parenthèses :

$$ \int\frac(11dx)((4x+19)^8)=\int\frac(11dx)(\left(4\left(x+\frac(19)(4)\right)\right)^ 8)= \int\frac(11dx)(4^8\left(x+\frac(19)(4)\right)^8)=\int\frac(\frac(11)(4^8)dx) (\left(x+\frac(19)(4)\right)^8). $$

Il est maintenant temps d'appliquer la formule :

$$ \int\frac(\frac(11)(4^8)dx)(\left(x+\frac(19)(4)\right)^8)=-\frac(\frac(11)(4 ^8))((8-1)\left(x+\frac(19)(4) \right)^(8-1))+C= -\frac(\frac(11)(4^8)) (7\left(x+\frac(19)(4) \right)^7)+C=-\frac(11)(7\cdot 4^8 \left(x+\frac(19)(4) \right )^7)+C. $$

Vous pouvez vous passer de la formule. Et même sans retirer les 4$ constants des parenthèses. Si l'on prend en compte que $dx=\frac(1)(4)d(4x+19)$, on obtient :

$$ \int\frac(11dx)((4x+19)^8)=11\int\frac(dx)((4x+19)^8)=\frac(11)(4)\int\frac( d(4x+19))((4x+19)^8)=|u=4x+19|=\\ =\frac(11)(4)\int\frac(du)(u^8)=\ frac(11)(4)\int u^(-8)\;du=\frac(11)(4)\cdot\frac(u^(-8+1))(-8+1)+C= \\ =\frac(11)(4)\cdot\frac(u^(-7))(-7)+C=-\frac(11)(28)\cdot\frac(1)(u^7 )+C=-\frac(11)(28(4x+19)^7)+C. $$

Des explications détaillées pour trouver de telles intégrales sont données dans le thème « Intégration par substitution (substitution sous le signe différentiel) ».

3) Nous devons intégrer la fraction $\frac(4x+7)(x^2+10x+34)$. Cette fraction a la structure $\frac(Mx+N)(x^2+px+q)$, où $M=4$, $N=7$, $p=10$, $q=34$. Cependant, pour s'assurer qu'il s'agit bien d'une fraction élémentaire du troisième type, il faut vérifier que la condition $p^2-4q est remplie< 0$. Так как $p^2-4q=10^2-4\cdot 34=-16 < 0$, то мы действительно имеем дело с интегрированием элементарной дроби третьего типа. Как и в предыдущих пунктах есть два пути для нахождения $\int\frac{4x+7}{x^2+10x+34}dx$. Первый путь - банально использовать формулу . Подставив в неё $M=4$, $N=7$, $p=10$, $q=34$ получим:

$$ \int\frac(4x+7)(x^2+10x+34)dx = \frac(4)(2)\cdot \ln (x^2+10x+34)+\frac(2\cdot 7-4\cdot 10)(\sqrt(4\cdot 34-10^2)) \arctg\frac(2x+10)(\sqrt(4\cdot 34-10^2))+C=\\ = 2\cdot \ln (x^2+10x+34)+\frac(-26)(\sqrt(36)) \arctg\frac(2x+10)(\sqrt(36))+C =2\cdot \ln (x^2+10x+34)+\frac(-26)(6) \arctg\frac(2x+10)(6)+C=\\ =2\cdot \ln (x^2+10x +34)-\frac(13)(3) \arctg\frac(x+5)(3)+C. $$

Résolvons le même exemple, mais sans utiliser de formule toute faite. Essayons d'isoler la dérivée du dénominateur au numérateur. Qu'est-ce que cela signifie? On sait que $(x^2+10x+34)"=2x+10$. C'est l'expression $2x+10$ qu'il faut isoler au numérateur. Pour l'instant le numérateur ne contient que $4x+7$, mais cela ne durera pas longtemps. Appliquons au numérateur la transformation suivante :

$$ 4x+7=2\cdot 2x+7=2\cdot (2x+10-10)+7=2\cdot(2x+10)-2\cdot 10+7=2\cdot(2x+10) -13. $$

Maintenant, l'expression requise $2x+10$ apparaît au numérateur. Et notre intégrale peut être réécrite comme suit :

$$ \int\frac(4x+7)(x^2+10x+34) dx= \int\frac(2\cdot(2x+10)-13)(x^2+10x+34)dx. $$

Divisons l'intégrande en deux. Eh bien, et, en conséquence, l'intégrale elle-même est également « bifurquée » :

$$ \int\frac(2\cdot(2x+10)-13)(x^2+10x+34)dx=\int \left(\frac(2\cdot(2x+10))(x^2 +10x+34)-\frac(13)(x^2+10x+34) \right)\; dx=\\ =\int \frac(2\cdot(2x+10))(x^2+10x+34)dx-\int\frac(13dx)(x^2+10x+34)=2\cdot \int \frac((2x+10)dx)(x^2+10x+34)-13\cdot\int\frac(dx)(x^2+10x+34). $$

Parlons d'abord de la première intégrale, c'est-à-dire à propos de $\int \frac((2x+10)dx)(x^2+10x+34)$. Puisque $d(x^2+10x+34)=(x^2+10x+34)"dx=(2x+10)dx$, alors le numérateur de l'intégrande contient la différentielle du dénominateur. En bref, à la place de l'expression $( 2x+10)dx$ on écrit $d(x^2+10x+34)$.

Disons maintenant quelques mots sur la deuxième intégrale. Sélectionnons un carré complet au dénominateur : $x^2+10x+34=(x+5)^2+9$. De plus, on prend en compte $dx=d(x+5)$. Maintenant, la somme des intégrales que nous avons obtenue plus tôt peut être réécrite sous une forme légèrement différente :

$$ 2\cdot\int \frac((2x+10)dx)(x^2+10x+34)-13\cdot\int\frac(dx)(x^2+10x+34) =2\cdot \int \frac(d(x^2+10x+34))(x^2+10x+34)-13\cdot\int\frac(d(x+5))((x+5)^2+ 9). $$

Si l'on fait le remplacement $u=x^2+10x+34$ dans la première intégrale, alors il prendra la forme $\int\frac(du)(u)$ et pourra être obtenu en appliquant simplement la deuxième formule de . Quant à la deuxième intégrale, le changement $u=x+5$ lui est réalisable, après quoi il prendra la forme $\int\frac(du)(u^2+9)$. Il s'agit de la onzième formule la plus pure du tableau des intégrales indéfinies. Donc, en revenant à la somme des intégrales, on a :

$$ 2\cdot\int \frac(d(x^2+10x+34))(x^2+10x+34)-13\cdot\int\frac(d(x+5))((x+ 5 )^2+9) =2\cdot\ln(x^2+10x+34)-\frac(13)(3)\arctg\frac(x+5)(3)+C. $$

Nous avons obtenu la même réponse que lors de l’application de la formule, ce qui, à proprement parler, n’est pas surprenant. En général, la formule est prouvée par les mêmes méthodes que celles utilisées pour trouver cette intégrale. Je pense que le lecteur attentif peut avoir une question ici, je vais donc la formuler :

Question n°1

Si nous appliquons la deuxième formule du tableau des intégrales indéfinies à l'intégrale $\int \frac(d(x^2+10x+34))(x^2+10x+34)$, alors nous obtenons ce qui suit :

$$ \int \frac(d(x^2+10x+34))(x^2+10x+34)=|u=x^2+10x+34|=\int\frac(du)(u) =\ln|u|+C=\ln|x^2+10x+34|+C. $$

Pourquoi n’y avait-il aucun module dans la solution ?

Réponse à la question n°1

La question est tout à fait naturelle. Le module manquait uniquement parce que l'expression $x^2+10x+34$ pour tout $x\in R$ est supérieure à zéro. Ceci est assez facile à démontrer de plusieurs manières. Par exemple, puisque $x^2+10x+34=(x+5)^2+9$ et $(x+5)^2 ≥ 0$, alors $(x+5)^2+9 > 0$ . Vous pouvez penser différemment, sans recourir à la sélection d’un carré complet. Depuis 10$^2-4\cdot 34=-16< 0$, то $x^2+10x+34 >0$ pour tout $x\in R$ (si cette chaîne logique est surprenante, je vous conseille de regarder la méthode graphique de résolution des inégalités quadratiques). Dans tous les cas, puisque $x^2+10x+34 > 0$, alors $|x^2+10x+34|=x^2+10x+34$, c'est-à-dire Au lieu d'un module, vous pouvez utiliser des supports ordinaires.

Tous les points de l'exemple n°1 ont été résolus, il ne reste plus qu'à noter la réponse.

Répondre:

1. $\int\frac(7dx)(x+9)=7\ln|x+9|+C$;
2. $\int\frac(11dx)((4x+19)^8)=-\frac(11)(28(4x+19)^7)+C$;
3. $\int\frac(4x+7)(x^2+10x+34)dx=2\cdot\ln(x^2+10x+34)-\frac(13)(3)\arctg\frac(x +5)(3)+$CAN.

Exemple n°2

Trouvez l'intégrale $\int\frac(7x+12)(3x^2-5x-2)dx$.

À première vue, la fraction intégrande $\frac(7x+12)(3x^2-5x-2)$ est très similaire à une fraction élémentaire du troisième type, c'est-à-dire par $\frac(Mx+N)(x^2+px+q)$. Il semble que la seule différence soit le coefficient de $3$ devant $x^2$, mais il ne faut pas longtemps pour supprimer le coefficient (le mettre hors parenthèses). Pourtant, cette similitude est évidente. Pour la fraction $\frac(Mx+N)(x^2+px+q)$ la condition $p^2-4q est obligatoire< 0$, которое гарантирует, что знаменатель $x^2+px+q$ нельзя разложить на множители. Проверим, как обстоит дело с разложением на множители у знаменателя нашей дроби, т.е. у многочлена $3x^2-5x-2$.

Notre coefficient avant $x^2$ n'est pas égal à un, vérifiez donc la condition $p^2-4q< 0$ напрямую мы не можем. Однако тут нужно вспомнить, откуда взялось выражение $p^2-4q$. Это всего лишь дискриминант квадратного уравнения $x^2+px+q=0$. Если дискриминант меньше нуля, то выражение $x^2+px+q$ на множители не разложишь. Вычислим дискриминант многочлена $3x^2-5x-2$, расположенного в знаменателе нашей дроби: $D=(-5)^2-4\cdot 3\cdot(-2)=49$. Итак, $D >0$, donc l'expression $3x^2-5x-2$ peut être factorisée. Cela signifie que la fraction $\frac(7x+12)(3x^2-5x-2)$ n'est pas une fraction élémentaire du troisième type, et applique $\int\frac(7x+12)(3x^2- ) à la formule intégrale 5x-2)dx$ n'est pas possible.

Eh bien, si la fraction rationnelle donnée n’est pas une fraction élémentaire, alors elle doit être représentée comme une somme de fractions élémentaires puis intégrée. Bref, profitez du sentier. Comment décomposer une fraction rationnelle en fractions élémentaires est écrit en détail. Commençons par factoriser le dénominateur :

$$ 3x^2-5x-2=0;\\ \begin(aligné) & D=(-5)^2-4\cdot 3\cdot(-2)=49;\\ & x_1=\frac( -(-5)-\sqrt(49))(2\cdot 3)=\frac(5-7)(6)=\frac(-2)(6)=-\frac(1)(3); \\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot 3)=\frac(5+7)(6)=\frac(12)(6)=2.\ \\end(aligné)\\ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)\cdot (x-2)= 3\cdot\left(x+\frac(1)(3)\right)(x-2). $$

Nous présentons la fraction subintercale sous cette forme :

$$ \frac(7x+12)(3x^2-5x-2)=\frac(7x+12)(3\cdot\left(x+\frac(1)(3)\right)(x-2) )=\frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2)). $$

Décomposons maintenant la fraction $\frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))$ en fractions élémentaires :

$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2)) =\frac(A)(x+\frac( 1)(3))+\frac(B)(x-2)=\frac(A(x-2)+B\left(x+\frac(1)(3)\right))(\left(x+ \frac(1)(3)\right)(x-2));\\ \frac(7)(3)x+4=A(x-2)+B\left(x+\frac(1)( 3)\droite). $$

Pour trouver les coefficients $A$ et $B$ il existe deux méthodes classiques : la méthode des coefficients indéterminés et la méthode de substitution de valeurs partielles. Appliquons la méthode de substitution de valeur partielle, en remplaçant $x=2$ puis $x=-\frac(1)(3)$ :

$$ \frac(7)(3)x+4=A(x-2)+B\left(x+\frac(1)(3)\right).\\ x=2;\; \frac(7)(3)\cdot 2+4=A(2-2)+B\left(2+\frac(1)(3)\right); \; \frac(26)(3)=\frac(7)(3)B;\; B=\frac(26)(7).\\ x=-\frac(1)(3);\; \frac(7)(3)\cdot \left(-\frac(1)(3) \right)+4=A\left(-\frac(1)(3)-2\right)+B\left (-\frac(1)(3)+\frac(1)(3)\right); \; \frac(29)(9)=-\frac(7)(3)A;\; A=-\frac(29\cdot 3)(9\cdot 7)=-\frac(29)(21).\\ $$

Une fois les coefficients trouvés, il ne reste plus qu'à noter le développement terminé :

$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=\frac(-\frac(29)( 21))(x+\frac(1)(3))+\frac(\frac(26)(7))(x-2). $$

En principe, vous pouvez laisser cette entrée, mais j'aime une option plus précise :

$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=-\frac(29)(21)\ cdot\frac(1)(x+\frac(1)(3))+\frac(26)(7)\cdot\frac(1)(x-2). $$

Revenant à l'intégrale d'origine, nous y substituons le développement résultant. Ensuite, nous divisons l’intégrale en deux et appliquons la formule à chacune. Je préfère placer immédiatement les constantes en dehors du signe intégral :

$$ \int\frac(7x+12)(3x^2-5x-2)dx =\int\left(-\frac(29)(21)\cdot\frac(1)(x+\frac(1) (3))+\frac(26)(7)\cdot\frac(1)(x-2)\right)dx=\\ =\int\left(-\frac(29)(21)\cdot\ frac(1)(x+\frac(1)(3))\right)dx+\int\left(\frac(26)(7)\cdot\frac(1)(x-2)\right)dx =- \frac(29)(21)\cdot\int\frac(dx)(x+\frac(1)(3))+\frac(26)(7)\cdot\int\frac(dx)(x-2 )dx=\\ =-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\right|+\frac(26)(7)\cdot\ln|x- 2|+C. $$

Répondre: $\int\frac(7x+12)(3x^2-5x-2)dx=-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\right| +\frac(26)(7)\cdot\ln|x-2|+C$.

Exemple n°3

Trouvez l'intégrale $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx$.

Nous devons intégrer la fraction $\frac(x^2-38x+157)((x-1)(x+4)(x-9))$. Le numérateur contient un polynôme du deuxième degré et le dénominateur contient un polynôme du troisième degré. Puisque le degré du polynôme au numérateur est inférieur au degré du polynôme au dénominateur, c'est-à-dire 2 $< 3$, то подынтегральная дробь является правильной. Разложение этой дроби на элементарные (простейшие) было получено в примере №3 на странице, посвящённой разложению рациональных дробей на элементарные. Полученное разложение таково:

$$ \frac(x^2-38x+157)((x-1)(x+4)(x-9))=-\frac(3)(x-1)+\frac(5)(x +4)-\frac(1)(x-9). $$

Tout ce que nous avons à faire est de diviser l’intégrale donnée en trois et d’appliquer la formule à chacune. Je préfère placer immédiatement les constantes en dehors du signe intégral :

$$ \int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=\int\left(-\frac(3)(x-1) +\frac(5)(x+4)-\frac(1)(x-9) \right)dx=\\=-3\cdot\int\frac(dx)(x-1)+ 5\cdot \int\frac(dx)(x+4)-\int\frac(dx)(x-9)=-3\ln|x-1|+5\ln|x+4|-\ln|x- 9|+C. $$

Répondre: $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=-3\ln|x-1|+5\ln|x+ 4 |-\ln|x-9|+C$.

La suite de l'analyse d'exemples de ce sujet se situe dans la deuxième partie.

Intégration de fonctions rationnelles Fractionnaire - fonction rationnelle Les fractions rationnelles les plus simples Décomposition d'une fraction rationnelle en fractions simples Intégration de fractions simples Règle générale pour l'intégration de fractions rationnelles

polynôme de degré n. Fonction fractionnaire - rationnelle Une fonction fractionnaire - rationnelle est une fonction égale au rapport de deux polynômes : Une fraction rationnelle est dite propre si le degré du numérateur est inférieur au degré du dénominateur, c'est-à-dire m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P

Fractionnel - fonction rationnelle Réduire une fraction impropre à la forme correcte : 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x

Fractions rationnelles les plus simples Fractions rationnelles propres de la forme : elles sont appelées fractions rationnelles les plus simples des types. hache A); 2(Nkk hache A k)04(2 2 qp qpxx NMx); 2 ; 04(2 2 Nkkqp qpxx NMx k V V,

Décomposition d'une fraction rationnelle en fractions simples Théorème : Toute fraction rationnelle propre dont le dénominateur est factorisé : peut par ailleurs être représentée de manière unique sous la forme d'une somme de fractions simples : s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx. M)(

Décomposition d'une fraction rationnelle en fractions simples Expliquons la formulation du théorème à l'aide des exemples suivants : Pour trouver les coefficients incertains A, B, C, D..., deux méthodes sont utilisées : la méthode de comparaison des coefficients et la méthode de valeurs partielles d'une variable. Examinons la première méthode à l'aide d'un exemple. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x

Décomposition d'une fraction rationnelle en fractions simples Présenter la fraction comme une somme de fractions simples : Ramenons les fractions les plus simples à un dénominateur commun Égaler les numérateurs des fractions résultantes et originales Égaler les coefficients aux mêmes puissances x)52)(1( 332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x

Intégration des fractions les plus simples Retrouvons les intégrales des fractions rationnelles les plus simples : Regardons l'intégration des fractions de type 3 à l'aide d'un exemple. dx hache A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k

Intégration de fractions simplesdx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 322 t dtt 9 9 2 3 2 2 t td 33 2 t arctg.C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln

Intégration de fractions simples Une intégrale de ce type par substitution : se réduit à la somme de deux intégrales : La première intégrale se calcule en introduisant t sous le signe différentiel. La deuxième intégrale est calculée à l'aide de la formule de récurrence : dx qpxx NMx k 2 V t p x 2 kk at dt N at dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt

Intégration de fractions simples a = 1 ; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t tarctg 2223)1)(13(2232 332 t t C t t tarctg 222)1 (4)1(

Règle générale pour intégrer des fractions rationnelles Si la fraction est impropre, représentez-la comme la somme d'un polynôme et d'une fraction propre. Après avoir factorisé le dénominateur d'une fraction rationnelle propre, représentez-la comme une somme de fractions simples avec des coefficients indéfinis.Trouver des coefficients indéfinis par la méthode de comparaison des coefficients ou par la méthode des valeurs partielles d'une variable. Intégrez le polynôme et la somme résultante de fractions simples.

Exemple Mettons la fraction sous la forme correcte. dx xxx 23 35 2 442 35 xxxxxx 2 2 2 x 345 2 xxx 442 34 xxx x 2 234 234 234 234 234 234 234 23 xxx xxx 23 35 2 442 xxx xx xx 23 2 2 48 52 5 xxx 5105 2 xx 2 xx 2 xx

Exemple Factorisons le dénominateur d'une fraction propre Représentons la fraction comme une somme de fractions simples Trouvons les coefficients indéterminés en utilisant la méthode des valeurs partielles de la variable xxx xx 23 2 2 48 2 2)1(48 xx xx 2 )1(1 x C x B x A 2 2)1 ()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx

Exemple dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln

Nous fournissons ici des solutions détaillées à trois exemples d’intégration des fractions rationnelles suivantes :
, , .

Exemple 1

Calculez l'intégrale :
.

Solution

Ici, sous le signe intégral se trouve une fonction rationnelle, puisque l'intégrande est une fraction de polynômes. Degré polynomial dénominateur ( 3 ) est inférieur au degré du polynôme numérateur ( 4 ). Par conséquent, vous devez d’abord sélectionner toute la partie de la fraction.

1. Sélectionnons toute la partie de la fraction. Diviser x 4 par x 3 - 6 x 2 + 11 x - 6:

D'ici
.

2. Factorisons le dénominateur de la fraction. Pour ce faire, vous devez résoudre l'équation cubique :
.
6
1, 2, 3, 6, -1, -2, -3, -6 .
Remplaçons x = 1 :
.

1 . Diviser par x - 1 :

D'ici
.
Résoudre une équation quadratique.
.
Les racines de l'équation sont : , .
Alors
.

3. Décomposons la fraction sous sa forme la plus simple.

.

Nous avons donc trouvé :
.
Intégrons.

Répondre

Exemple 2

Calculez l'intégrale :
.

Solution

Ici le numérateur de la fraction est un polynôme de degré zéro ( 1 = x0). Le dénominateur est un polynôme du troisième degré. Parce que le 0 < 3 , alors la fraction est correcte. Décomposons-le en fractions simples.

1. Factorisons le dénominateur de la fraction. Pour ce faire, vous devez résoudre l’équation du troisième degré :
.
Supposons qu'il possède au moins une racine entière. Alors c'est un diviseur du nombre 3 (membre sans x). C'est-à-dire que la racine entière peut être l'un des nombres :
1, 3, -1, -3 .
Remplaçons x = 1 :
.

Nous avons donc trouvé une racine x = 1 . Diviser x 3 + 2x-3 sur x - 1 :

Donc,
.

Résoudre l'équation quadratique :
X 2 + x + 3 = 0.
Trouver le discriminant : D = 1 2 - 4 3 = -11. Depuis D< 0 , alors l'équation n'a pas de vraies racines. Ainsi, nous avons obtenu la factorisation du dénominateur :
.

2.
.
(x - 1)(x 2 + x + 3):
(2.1) .
Remplaçons x = 1 . Alors x - 1 = 0 ,
.

Remplaçons (2.1) X = 0 :
1 = 3A-C;
.

Égalons à (2.1) coefficients pour x 2 :
;
0 = A + B;
.

.

3. Intégrons.
(2.2) .
Pour calculer la deuxième intégrale, on sélectionne la dérivée du dénominateur au numérateur et on réduit le dénominateur à la somme des carrés.

;
;
.

Calculer je 2 .


.
Puisque l'équation x 2 + x + 3 = 0 n'a pas de vraies racines, alors x 2 + x + 3 > 0. Le signe du module peut donc être omis.

Nous livrons à (2.2) :
.

Répondre

Exemple 3

Calculez l'intégrale :
.

Solution

Ici, sous le signe intégral se trouve une fraction de polynômes. L’intégrande est donc une fonction rationnelle. Le degré du polynôme au numérateur est égal à 3 . Le degré du polynôme du dénominateur de la fraction est égal à 4 . Parce que le 3 < 4 , alors la fraction est correcte. On peut donc le décomposer en fractions simples. Mais pour ce faire, vous devez factoriser le dénominateur.

1. Factorisons le dénominateur de la fraction. Pour ce faire, vous devez résoudre l’équation du quatrième degré :
.
Supposons qu'il possède au moins une racine entière. Alors c'est un diviseur du nombre 2 (membre sans x). C'est-à-dire que la racine entière peut être l'un des nombres :
1, 2, -1, -2 .
Remplaçons x = -1 :
.

Nous avons donc trouvé une racine x = -1 . Diviser par x - (-1) = x + 1:


Donc,
.

Il nous faut maintenant résoudre l’équation du troisième degré :
.
Si nous supposons que cette équation a une racine entière, alors c'est un diviseur du nombre 2 (membre sans x). C'est-à-dire que la racine entière peut être l'un des nombres :
1, 2, -1, -2 .
Remplaçons x = -1 :
.

Nous avons donc trouvé une autre racine x = -1 . Il serait possible, comme dans le cas précédent, de diviser le polynôme par , mais on regroupera les termes :
.

Puisque l'équation x 2 + 2 = 0 n'a pas de vraies racines, alors on obtient la factorisation du dénominateur :
.

2. Décomposons la fraction sous sa forme la plus simple. Nous recherchons une extension sous la forme :
.
On se débarrasse du dénominateur de la fraction, on multiplie par (x + 1) 2 (x 2 + 2):
(3.1) .
Remplaçons x = -1 . Alors x + 1 = 0 ,
.

Différencions (3.1) :

;

.
Remplaçons x = -1 et prendre en compte que x + 1 = 0 :
;
; .

Remplaçons (3.1) X = 0 :
0 = 2 A + 2 B + D;
.

Égalons à (3.1) coefficients pour x 3 :
;
1 = B + C;
.

Nous avons donc trouvé la décomposition en fractions simples :
.

3. Intégrons.


.

« Un mathématicien, tout comme un artiste ou un poète, crée des motifs. Et si ses motifs sont plus stables, c'est uniquement parce qu'ils sont composés d'idées... Les motifs d'un mathématicien, tout comme ceux d'un artiste ou d'un poète, doivent être beaux ; Les idées, tout comme les couleurs ou les mots, doivent se correspondre. La beauté est la première exigence : il n’y a pas de place au monde pour les mathématiques laides».

G.H. Hardy

Dans le premier chapitre, il a été noté qu'il existe des primitives de fonctions assez simples qui ne peuvent plus être exprimées par des fonctions élémentaires. À cet égard, les classes de fonctions dont nous pouvons dire avec précision que leurs primitives sont des fonctions élémentaires acquièrent une énorme importance pratique. Cette classe de fonctions comprend fonctions rationnelles, représentant le rapport de deux polynômes algébriques. De nombreux problèmes conduisent à l’intégration de fractions rationnelles. Il est donc très important de pouvoir intégrer de telles fonctions.

2.1.1. Fonctions rationnelles fractionnaires

Fraction rationnelle(ou fonction rationnelle fractionnaire) est appelée la relation de deux polynômes algébriques :

où et sont des polynômes.

Rappelons que polynôme (polynôme, fonction rationnelle entière) nème degré appelée fonction de la forme

Où - nombres réels. Par exemple,

– polynôme du premier degré ;

– polynôme du quatrième degré, etc.

La fraction rationnelle (2.1.1) s'appelle correct, si le diplôme est inférieur au diplôme , c'est-à-dire n<m, sinon la fraction s'appelle faux.

Toute fraction impropre peut être représentée comme la somme d'un polynôme (la partie entière) et d'une fraction propre (la partie fractionnaire). La séparation des parties entières et fractionnaires d'une fraction impropre peut se faire selon la règle de division des polynômes par un « coin ».

Exemple 2.1.1. Identifiez les parties entières et fractionnaires des fractions rationnelles impropres suivantes :

UN) 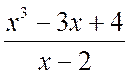, b) .

Solution . a) En utilisant l’algorithme de division « coin », on obtient

Ainsi, nous obtenons

.

b) Ici, nous utilisons également l'algorithme de division « coin » :

En conséquence, nous obtenons

.

Résumons. Dans le cas général, l'intégrale indéfinie d'une fraction rationnelle peut être représentée comme la somme des intégrales du polynôme et de la fraction rationnelle propre. Trouver des primitives de polynômes n’est pas difficile. Par conséquent, dans ce qui suit, nous considérerons principalement les fractions rationnelles propres.

2.1.2. Les fractions rationnelles les plus simples et leur intégration

Parmi les fractions rationnelles propres, il existe quatre types, classés comme suit : les fractions rationnelles (élémentaires) les plus simples :

3) ,

4) ,

où est un entier, , c'est à dire. trinôme quadratique n'a pas de véritables racines.

L'intégration de fractions simples du 1er et du 2ème types ne présente pas de grandes difficultés :

, (2.1.3)

. (2.1.4)

Considérons maintenant l'intégration de fractions simples du 3ème type, mais nous ne considérerons pas les fractions du 4ème type.

Commençons par les intégrales de la forme

.

Cette intégrale est généralement calculée en isolant le carré parfait du dénominateur. Le résultat est un tableau intégral de la forme suivante

ou .

Exemple 2.1.2. Trouvez les intégrales :

UN) , b) .

Solution . a) Sélectionnez un carré complet à partir d'un trinôme quadratique :

De là, nous trouvons

b) En isolant un carré complet d'un trinôme quadratique, on obtient :

Ainsi,

.

Pour trouver l'intégrale

vous pouvez isoler la dérivée du dénominateur au numérateur et développer l'intégrale en la somme de deux intégrales : la première d'entre elles par substitution ça se résume à l'apparence

,

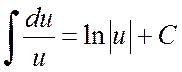et le second - à celui discuté ci-dessus.

Exemple 2.1.3. Trouvez les intégrales :

.

Solution . remarquerez que 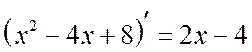. Isolons la dérivée du dénominateur au numérateur :

La première intégrale est calculée en utilisant la substitution :

Dans la deuxième intégrale, on sélectionne le carré parfait au dénominateur

Finalement, nous obtenons

2.1.3. Expansion rationnelle des fractions
pour la somme de fractions simples

Toute fraction rationnelle appropriée peut être représenté de manière unique comme une somme de fractions simples. Pour ce faire, le dénominateur doit être factorisé. De l'algèbre supérieure, on sait que tout polynôme à coefficients réels

Une fonction rationnelle est une fraction de la forme dont le numérateur et le dénominateur sont des polynômes ou des produits de polynômes.

Exemple 1. Étape 2.

.

On multiplie les coefficients indéterminés par des polynômes qui ne sont pas dans cette fraction individuelle, mais qui sont dans d'autres fractions résultantes :

Nous ouvrons les parenthèses et assimilons le numérateur de l'intégrande d'origine à l'expression résultante :

Des deux côtés de l'égalité, nous recherchons des termes avec les mêmes puissances de x et composons à partir d'eux un système d'équations :

.

On annule tous les x et on obtient un système d’équations équivalent :

.

Ainsi, le développement final de l’intégrande en une somme de fractions simples est :

.

Exemple 2. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Nous commençons maintenant à rechercher des coefficients incertains. Pour ce faire, nous assimilons le numérateur de la fraction d'origine dans l'expression de la fonction au numérateur de l'expression obtenue après réduction de la somme des fractions à un dénominateur commun :

Vous devez maintenant créer et résoudre un système d’équations. Pour ce faire, on assimile les coefficients de la variable au degré correspondant au numérateur de l'expression originale de la fonction et aux coefficients similaires dans l'expression obtenue à l'étape précédente :

On résout le système résultant :

Donc, à partir d'ici

.

Exemple 3. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

Nous commençons à rechercher des coefficients incertains. Pour ce faire, nous assimilons le numérateur de la fraction d'origine dans l'expression de la fonction au numérateur de l'expression obtenue après réduction de la somme des fractions à un dénominateur commun :

Comme dans les exemples précédents, nous composons un système d'équations :

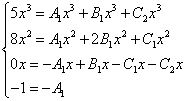
Nous réduisons les x et obtenons un système d'équations équivalent :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 4. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Nous savons déjà grâce aux exemples précédents comment assimiler le numérateur de la fraction originale à l'expression au numérateur obtenue après avoir décomposé la fraction en la somme de fractions simples et ramené cette somme à un dénominateur commun. Par conséquent, juste à des fins de contrôle, nous présentons le système d’équations résultant :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

Exemple 5. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Nous réduisons indépendamment cette somme à un dénominateur commun, assimilant le numérateur de cette expression au numérateur de la fraction originale. Le résultat devrait être le système d’équations suivant :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

.

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 6. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

Nous effectuons les mêmes actions avec ce montant que dans les exemples précédents. Le résultat devrait être le système d’équations suivant :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

.

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 7. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Après certaines actions avec le montant résultant, le système d'équations suivant doit être obtenu :

En résolvant le système, on obtient les valeurs suivantes des coefficients incertains :

On obtient la décomposition finale de l'intégrande en somme de fractions simples :

.

Exemple 8. Étape 2. A l'étape 1, nous avons obtenu la décomposition suivante de la fraction originale en somme de fractions simples à coefficients indéterminés aux numérateurs :

.

Apportons quelques modifications aux actions qui ont déjà été amenées à l'automaticité pour obtenir un système d'équations. Il existe une technique artificielle qui, dans certains cas, permet d'éviter des calculs inutiles. En ramenant la somme des fractions à un dénominateur commun, on obtient et en assimilant le numérateur de cette expression au numérateur de la fraction originale, on obtient.