CHAPITRE III.
DÉCIMAUX.
§ 31. Problèmes et exemples pour toutes les opérations avec des fractions décimales.
Suivez ces étapes:

767. Trouvez le quotient de division :
Suivez ces étapes:

772. Calculer:
Trouver X , Si:

776. Le nombre inconnu a été multiplié par la différence entre les nombres 1 et 0,57 et le produit était 3,44. Trouvez le numéro inconnu.
777. La somme du nombre inconnu et de 0,9 a été multipliée par la différence entre 1 et 0,4 et le produit était de 2,412. Trouvez le numéro inconnu.
778. À l'aide des données du diagramme sur la fonte du fer dans la RSFSR (Fig. 36), créez un problème à résoudre auquel vous devez appliquer les actions d'addition, de soustraction et de division.

779. 1) La longueur du canal de Suez est de 165,8 km, la longueur du canal de Panama est inférieure de 84,7 km à celle du canal de Suez et la longueur du canal mer Blanche-Baltique est supérieure de 145,9 km à celle du canal de Panama. Quelle est la longueur du canal Mer Blanche-Baltique ?
2) Le métro de Moscou (en 1959) a été construit en 5 étapes. La longueur de la première étape du métro est de 11,6 km, la deuxième de 14,9 km, la longueur de la troisième est de 1,1 km inférieure à la longueur de la deuxième étape, la longueur de la quatrième étape est de 9,6 km de plus que la troisième étape , et la longueur de la cinquième étape est de 11,5 km moins la quatrième. Quelle était la longueur du métro de Moscou au début de 1959 ?
780. 1) La plus grande profondeur de l'océan Atlantique est de 8,5 km, la plus grande profondeur de l'océan Pacifique est de 2,3 km supérieure à la profondeur de l'océan Atlantique et la plus grande profondeur de l'océan Arctique est 2 fois inférieure à la plus grande profondeur de l'océan Atlantique. Océan Pacifique. Quelle est la plus grande profondeur de l’océan Arctique ?
2) La voiture Moskvich consomme 9 litres d'essence aux 100 km, la voiture Pobeda consomme 4,5 litres de plus que la Moskvich et la Volga 1,1 fois plus que la Pobeda. Combien d'essence consomme une voiture Volga pour 1 km de trajet ? (Arrondissez la réponse à 0,01 l près.)
781. 1) L'étudiant est allé chez son grand-père pendant les vacances. Il a voyagé en train pendant 8,5 heures et depuis la gare à cheval pendant 1,5 heure. Au total, il a parcouru 440 km. À quelle vitesse l'étudiant voyageait-il sur le chemin de fer s'il montait à cheval à une vitesse de 10 km/h ?
2) Le kolkhozien devait se trouver en un point situé à 134,7 km de son domicile. Il a pris le bus pendant 2,4 heures à une vitesse moyenne de 55 km/h et a parcouru le reste du trajet à pied à une vitesse de 4,5 km/h. Combien de temps a-t-il marché ?
782. 1) Au cours de l'été, un spermophile détruit environ 0,12 centième de pain. Au printemps, les pionniers ont exterminé 1 250 spermophiles sur 37,5 hectares. Combien de pain les écoliers ont-ils économisé pour la ferme collective ? Combien y a-t-il de pain économisé pour 1 hectare ?
2) La ferme collective a calculé qu'en détruisant les gaufres sur une superficie de 15 hectares de terres arables, les écoliers ont économisé 3,6 tonnes de céréales. Combien de spermophiles sont détruits en moyenne par hectare de terre si un gaufre détruit 0,012 tonne de céréales au cours de l'été ?
783. 1) Lors de la mouture du blé en farine, 0,1 de son poids est perdu et lors de la cuisson, une cuisson égale à 0,4 du poids de farine est obtenue. Quelle quantité de pain cuit sera produite à partir de 2,5 tonnes de blé ?
2) La ferme collective a collecté 560 tonnes de graines de tournesol. Quelle quantité d'huile de tournesol sera produite à partir des grains collectés si le poids du grain est 0,7 du poids des graines de tournesol et le poids de l'huile obtenue est 0,25 du poids du grain ?
784. 1) Le rendement en crème du lait est de 0,16 du poids de lait et le rendement en beurre de la crème est de 0,25 du poids de la crème. Quelle quantité de lait (en poids) faut-il pour produire 1 quintal de beurre ?
2) Combien de kilogrammes de cèpes faut-il collecter pour obtenir 1 kg de champignons séchés, s'il reste lors de la préparation au séchage 0,5 du poids, et lors du séchage 0,1 du poids du champignon transformé ?
785. 1) Les terres attribuées à la ferme collective sont utilisées comme suit : 55 % d'entre elles sont occupées par des terres arables, 35 % par des prairies, et le reste des terres d'un montant de 330,2 hectares est affecté au jardin de la ferme collective et à les domaines des kolkhoziens. Combien de terres y a-t-il dans la ferme collective ?
2) La ferme collective a ensemencé 75 % de la superficie totale ensemencée en céréales, 20 % en légumes et le reste en graminées fourragères. Quelle superficie ensemencée aurait la ferme collective si elle ensemençait 60 hectares de graminées fourragères ?
786. 1) Combien de quintaux de graines faudra-t-il pour semer un champ en forme de rectangle de 875 m de long et 640 m de large, si l'on sème 1,5 quintaux de graines pour 1 hectare ?
2) Combien de quintaux de graines faudra-t-il pour semer un champ en forme de rectangle si son périmètre est de 1,6 km ? La largeur du champ est de 300 m. Pour semer 1 hectare, il faut 1,5 quintal de graines.
787. Combien de plaques carrées d'un côté de 0,2 dm peuvent tenir dans un rectangle mesurant 0,4 dm x 10 dm ?
788. La salle de lecture a des dimensions de 9,6 mx 5 mx 4,5 m. Pour combien de places la salle de lecture est-elle conçue si 3 mètres cubes sont nécessaires pour chaque personne ? m d'air ?
789. 1) Quelle surface de prairie un tracteur équipé d'une remorque de quatre faucheuses peut-il tondre en 8 heures, si la largeur de travail de chaque faucheuse est de 1,56 m et la vitesse du tracteur est de 4,5 km/h ? (Le temps d'arrêt n'est pas pris en compte.) (Arrondissez la réponse au 0,1 hectare le plus proche.)
2) La largeur de travail du semoir de légumes tracteur est de 2,8 m. Quelle superficie peut être semée avec ce semoir en 8 heures. travailler à une vitesse de 5 km/h ?
790. 1) Déterminez le rendement d’une charrue tracteur à trois corps en 10 heures. travail, si la vitesse du tracteur est de 5 km par heure, l'adhérence d'un corps est de 35 cm et la perte de temps était de 0,1 du temps total passé. (Arrondissez la réponse au 0,1 hectare le plus proche.)
2) Trouver le rendement d'une charrue tracteur à cinq corps en 6 heures. travail, si la vitesse du tracteur est de 4,5 km par heure, l'adhérence d'un corps est de 30 cm et la perte de temps était de 0,1 du temps total passé. (Arrondissez la réponse au 0,1 hectare le plus proche.)
791. La consommation d'eau par 5 km de trajet pour une locomotive à vapeur d'un train de voyageurs est de 0,75 tonne, le réservoir d'eau du tendre contient 16,5 tonnes d'eau. Combien de kilomètres le train aura-t-il suffisamment d’eau pour parcourir si le réservoir est rempli à 0,9 de sa capacité ?
792. La voie d'évitement ne peut accueillir que 120 wagons de marchandises d'une longueur moyenne de 7,6 m. Combien de wagons de voyageurs à quatre essieux, chacun mesurant 19,2 m de long, peuvent tenir sur cette voie si 24 wagons de marchandises supplémentaires sont placés sur cette voie ?
793. Pour assurer la solidité du remblai ferroviaire, il est recommandé de renforcer les pentes en semant des graminées des champs. Pour chaque mètre carré de remblai, il faut 2,8 g de graines, ce qui coûte 0,25 rouble. pour 1 kg. Combien coûtera le semis de 1,02 hectares de talus si le coût des travaux est 0,4 du coût des semences ? (Arrondissez la réponse au rouble le plus proche.)
794. La briqueterie livrait des briques à la gare. 25 chevaux et 10 camions ont travaillé pour transporter les briques. Chaque cheval transportait 0,7 tonne par voyage et effectuait 4 voyages par jour. Chaque véhicule transportait 2,5 tonnes par trajet et effectuait 15 déplacements par jour. Le transport a duré 4 jours. Combien de briques ont été livrées à la gare si le poids moyen d'une brique est de 3,75 kg ? (Arrondissez la réponse au millier d’unités le plus proche.)
795. Le stock de farine était réparti entre trois boulangeries : la première recevait 0,4 du stock total, la deuxième 0,4 du reste et la troisième boulangerie recevait 1,6 tonne de farine de moins que la première. Quelle quantité de farine a été distribuée au total ?
796. En deuxième année de l'institut, il y a 176 étudiants, en troisième année il y en a 0,875 et en première année il y en a une fois et demie plus qu'en troisième année. Le nombre d'étudiants en première, deuxième et troisième années représentait 0,75 du nombre total d'étudiants de cet institut. Combien d’étudiants y avait-il à l’institut ?
797. Trouvez la moyenne arithmétique :
1) deux nombres : 56,8 et 53,4 ; 705.3 et 707.5 ;
2) trois nombres : 46,5 ; 37,8 et 36 ; 0,84 ; 0,69 et 0,81 ;
3) quatre nombres : 5,48 ; 1,36 ; 3.24 et 2.04.
798. 1) Le matin la température était de 13,6°, à midi de 25,5° et le soir de 15,2°. Calculez la température moyenne pour cette journée.
2) Quelle est la température moyenne pour la semaine, si pendant la semaine le thermomètre indiquait : 21° ; 20,3°; 22,2°; 23,5°; 21,1° ; 22,1° ; 20,8° ?
799. 1) L'équipe de l'école a désherbé 4,2 hectares de betteraves le premier jour, 3,9 hectares le deuxième jour et 4,5 hectares le troisième. Déterminez le rendement moyen de l’équipe par jour.
2) Pour établir le délai standard de fabrication d'une nouvelle pièce, 3 tourneurs ont été fournis. Le premier a produit la pièce en 3,2 minutes, le deuxième en 3,8 minutes et le troisième en 4,1 minutes. Calculez la norme de temps qui a été définie pour la fabrication de la pièce.
800. 1) La moyenne arithmétique de deux nombres est 36,4. L'un de ces nombres est 36,8. Trouvez autre chose.
2) La température de l'air a été mesurée trois fois par jour : le matin, à midi et le soir. Trouvez la température de l'air le matin s'il faisait 28,4° à midi, 18,2° le soir et que la température moyenne du jour est de 20,4°.
801. 1) La voiture a parcouru 98,5 km au cours des deux premières heures et 138 km au cours des trois heures suivantes. Combien de kilomètres une voiture moyenne parcourt-elle par heure ?
2) Un test de capture et de pesée de carpes d'un an a montré que sur 10 carpes, 4 pesaient 0,6 kg, 3 pesaient 0,65 kg, 2 pesaient 0,7 kg et 1 pesait 0,8 kg. Quel est le poids moyen d’une carpe d’un an ?
802. 1) Pour 2 litres de sirop coûte 1,05 roubles. pour 1 litre, ajoutez 8 litres d'eau. Combien coûte 1 litre de l'eau obtenue avec du sirop ?
2) L'hôtesse a acheté une boîte de 0,5 litre de bortsch en conserve pour 36 kopecks. et bouilli avec 1,5 litre d'eau. Combien coûte une assiette de bortsch si son volume est de 0,5 litre ?
803. Travaux de laboratoire « Mesure de la distance entre deux points »,
1er rendez-vous. Mesure avec un ruban à mesurer (ruban à mesurer). La classe est divisée en unités de trois personnes chacune. Accessoires : 5-6 pôles et 8-10 tags.
Avancement des travaux : 1) les points A et B sont marqués et une ligne droite est tracée entre eux (voir tâche 178) ; 2) poser le mètre ruban le long de la ligne droite accrochée et marquer à chaque fois l'extrémité du mètre ruban avec une étiquette. 2ème rendez-vous. Mesure, étapes. La classe est divisée en unités de trois personnes chacune. Chaque élève parcourt la distance de A à B en comptant le nombre de ses pas. En multipliant la longueur moyenne de votre pas par le nombre de pas obtenu, vous trouvez la distance de A à B.
3ème rendez-vous. Mesure à l'oeil. Chaque élève tend la main gauche avec le pouce levé (Fig. 37) et pointe son pouce vers le poteau au point B (un arbre sur la photo) de manière à ce que l'œil gauche (point A), le pouce et le point B soient sur le même ligne droite. Sans changer de position, fermez votre œil gauche et regardez votre pouce avec votre droit. Mesurez le déplacement résultant à l'œil nu et augmentez-le de 10 fois. C'est la distance de A à B.

804. 1) Selon le recensement de 1959, la population de l'URSS était de 208,8 millions d'habitants et la population rurale était de 9,2 millions de plus que la population urbaine. Combien y avait-il de citadins et de ruraux en URSS en 1959 ?
2) Selon le recensement de 1913, la population de la Russie était de 159,2 millions d'habitants et la population urbaine était inférieure de 103,0 millions à la population rurale. Quelle était la population urbaine et rurale en Russie en 1913 ?
805. 1) La longueur du fil est de 24,5 m. Ce fil a été coupé en deux parties de sorte que la première partie soit 6,8 m plus longue que la seconde. Combien de mètres mesure chaque pièce ?
2) La somme de deux nombres est 100,05. Un nombre est 97,06 de plus que l’autre. Trouvez ces numéros.
806. 1) Il y a 8656,2 tonnes de charbon dans trois entrepôts de charbon, dans le deuxième entrepôt il y a 247,3 tonnes de charbon de plus que dans le premier et dans le troisième il y a 50,8 tonnes de plus que dans le second. Combien de tonnes de charbon y a-t-il dans chaque entrepôt ?
2) La somme de trois nombres est 446,73. Le premier nombre est inférieur au deuxième de 73,17 et supérieur au troisième de 32,22. Trouvez ces numéros.
807. 1) Le bateau s'est déplacé le long de la rivière à une vitesse de 14,5 km par heure et à contre-courant à une vitesse de 9,5 km par heure. Quelle est la vitesse du bateau en eau calme et quelle est la vitesse du courant de la rivière ?
2) Le paquebot a parcouru 85,6 km le long du fleuve en 4 heures, et 46,2 km à contre-courant en 3 heures. Quelle est la vitesse du bateau à vapeur en eau calme et quelle est la vitesse du courant de la rivière ?
808. 1) Deux navires à vapeur ont livré 3 500 tonnes de marchandises et un navire à vapeur a livré 1,5 fois plus de marchandises que l'autre. Quelle quantité de marchandises chaque navire transportait-il ?
2) La superficie de deux pièces est de 37,2 mètres carrés. m La superficie d'une pièce est 2 fois plus grande que l'autre. Quelle est la superficie de chaque pièce ?
809. 1) Depuis deux agglomérations distantes de 32,4 km, un motocycliste et un cycliste se sont dirigés simultanément l'un vers l'autre. Combien de kilomètres chacun d'eux parcourra-t-il avant le rendez-vous si la vitesse du motocycliste est 4 fois celle du cycliste ?
2) Trouvez deux nombres dont la somme est 26,35 et le quotient de la division d'un nombre par l'autre est 7,5.
810. 1) L'usine a envoyé trois types de marchandises d'un poids total de 19,2 tonnes. Le poids du premier type de marchandises était trois fois supérieur au poids du deuxième type de marchandises et le poids du troisième type de marchandises était deux fois moins élevé. comme le poids du premier et du deuxième types de marchandises combinés. Quel est le poids de chaque type de marchandise ?
2) En trois mois, une équipe de mineurs a extrait 52,5 mille tonnes de minerai de fer. En mars, il a été produit 1,3 fois, en février 1,2 fois plus qu'en janvier. Quelle quantité de minerai l’équipage a-t-il extrait chaque mois ?
811. 1) Le gazoduc Saratov-Moscou est plus long de 672 km que le canal de Moscou. Trouvez la longueur des deux structures si la longueur du gazoduc est 6,25 fois supérieure à la longueur du canal de Moscou.
2) La longueur de la rivière Don est 3,934 fois supérieure à la longueur de la rivière Moscou. Trouvez la longueur de chaque rivière si la longueur de la rivière Don est supérieure de 1 467 km à la longueur de la rivière Moscou.
812. 1) La différence entre deux nombres est 5,2 et le quotient d'un nombre divisé par un autre est 5. Trouvez ces nombres.
2) La différence entre deux nombres est de 0,96 et leur quotient est de 1,2. Trouvez ces numéros.
813. 1) Un nombre est 0,3 de moins que l’autre et en représente 0,75. Trouvez ces numéros.
2) Un nombre est 3,9 de plus qu’un autre nombre. Si le plus petit nombre est doublé, ce sera 0,5 du plus grand. Trouvez ces numéros.
814. 1) La ferme collective a semé 2 600 hectares de blé et de seigle. Combien d'hectares de terre ont été ensemencés en blé et combien en seigle, si 0,8 de la superficie ensemencée en blé est égal à 0,5 de la superficie ensemencée en seigle ?
2) La collection de deux garçons totalise 660 timbres. De combien de timbres la collection de chaque garçon est composée si 0,5 des timbres du premier garçon est égal à 0,6 de la collection du deuxième garçon ?
815. Deux étudiants avaient ensemble 5,4 roubles. Après que le premier ait dépensé 0,75 de son argent et le second 0,8 de son argent, il leur restait la même somme d’argent. De combien d’argent disposait chaque élève ?
816. 1) Deux bateaux à vapeur partent l'un vers l'autre de deux ports dont la distance est de 501,9 km. Combien de temps leur faudra-t-il pour se rencontrer si la vitesse du premier navire est de 25,5 km par heure et celle du second de 22,3 km par heure ?
2) Deux trains partent l'un vers l'autre de deux points dont la distance est de 382,2 km. Combien de temps leur faudra-t-il pour se rencontrer si la vitesse moyenne du premier train était de 52,8 km/h et celle du second de 56,4 km/h ?
817. 1) Deux voitures ont quitté deux villes situées à une distance de 462 km en même temps et se sont rencontrées au bout de 3,5 heures. Trouvez la vitesse de chaque voiture si la vitesse de la première était supérieure de 12 km/h à la vitesse de la deuxième voiture.
2) Depuis deux agglomérations distantes de 63 km, un motocycliste et un cycliste sont partis en même temps l'un vers l'autre et se sont rencontrés au bout de 1,2 heure. Trouvez la vitesse du motocycliste si le cycliste roulait à une vitesse inférieure de 27,5 km par heure à la vitesse du motocycliste.
818. L'étudiant a remarqué qu'un train composé d'une locomotive à vapeur et de 40 voitures est passé à côté de lui pendant 35 secondes. Déterminez la vitesse du train par heure si la longueur de la locomotive est de 18,5 m et la longueur du wagon est de 6,2 m. (Donnez la réponse avec une précision de 1 km par heure.)
819. 1) Un cycliste a quitté A pour B à une vitesse moyenne de 12,4 km/h. Après 3 heures 15 minutes. un autre cycliste est parti de B vers lui à une vitesse moyenne de 10,8 km/h. Au bout de combien d'heures et à quelle distance de A se retrouveront-ils si 0,32 la distance entre A et B est de 76 km ?
2) Depuis les villes A et B, distantes de 164,7 km, un camion de la ville A et une voiture de la ville B se sont dirigés l'un vers l'autre. La vitesse du camion est de 36 km et la vitesse de la voiture est de 1,25 fois. plus haut. La voiture particulière est repartie 1,2 heure plus tard que le camion. Au bout de combien de temps et à quelle distance de la ville B la voiture particulière rencontrera-t-elle le camion ?
820. Deux navires ont quitté le même port au même moment et font route dans la même direction. Le premier bateau à vapeur parcourt 37,5 km toutes les 1,5 heures et le deuxième bateau à vapeur parcourt 45 km toutes les 2 heures. Combien de temps faudra-t-il pour que le premier navire soit à 10 km du second ?
821. Un piéton a d'abord quitté un point, et 1h30 après sa sortie, un cycliste est parti dans la même direction. À quelle distance du point le cycliste a-t-il rattrapé le piéton si le piéton marchait à une vitesse de 4,25 km/h et le cycliste roulait à une vitesse de 17 km/h ?
822. Le train a quitté Moscou pour Leningrad à 6 heures. 10 minutes. matin et j'ai marché à une vitesse moyenne de 50 km/h. Plus tard, un avion de passagers a décollé de Moscou à destination de Léningrad et est arrivé à Léningrad en même temps que l'arrivée du train. La vitesse moyenne de l'avion était de 325 km par heure et la distance entre Moscou et Léningrad était de 650 km. Quand l’avion a-t-il décollé de Moscou ?
823. Le bateau à vapeur a parcouru le fleuve pendant 5 heures, et à contre-courant pendant 3 heures et n'a parcouru que 165 km. Combien de kilomètres a-t-il parcouru en aval et combien à contre-courant, si la vitesse du débit de la rivière est de 2,5 km par heure ?
824. Le train a quitté A et doit arriver à B à une certaine heure ; après avoir parcouru la moitié du chemin et parcouru 0,8 km en 1 minute, le train a été arrêté pendant 0,25 heure ; après avoir encore augmenté la vitesse de 100 m pour 1 million, le train est arrivé à l'heure à B. Trouvez la distance entre A et B.
825. De la ferme collective à la ville 23 km. Un facteur a roulé à vélo de la ville à la ferme collective à une vitesse de 12,5 km/h. Quatre heures plus tard, le directeur du kolkhoze est entré en ville à cheval à une vitesse égale à 0,6 de celle du facteur. Combien de temps après son départ le kolkhozien rencontrera-t-il le facteur ?
826. Une voiture a quitté la ville A pour la ville B, à 234 km de A, à une vitesse de 32 km/h. 1h75 plus tard, une deuxième voiture a quitté la ville B en direction de la première, dont la vitesse était 1,225 fois supérieure à la vitesse de la première. Combien d’heures après le départ la deuxième voiture rencontrera-t-elle la première ?
827. 1) Un dactylographe peut retaper un manuscrit en 1,6 heure et un autre en 2,5 heures. Combien de temps faudra-t-il aux deux dactylos pour taper ce manuscrit, en travaillant ensemble ? (Arrondissez la réponse à 0,1 heure près.)
2) La piscine est remplie de deux pompes de puissance différente. La première pompe, fonctionnant seule, peut remplir la piscine en 3,2 heures et la seconde en 4 heures. Combien de temps faudra-t-il pour remplir la piscine si ces pompes fonctionnent simultanément ? (Arrondissez la réponse à 0,1 près.)
828. 1) Une équipe peut finaliser une commande en 8 jours. L'autre a besoin de 0,5 fois pour terminer cette commande. La troisième équipe peut finaliser cette commande en 5 jours. Combien de jours faudra-t-il pour finaliser la totalité de la commande si trois équipes travaillent ensemble ? (Arrondissez la réponse à 0,1 jour près.)
2) Le premier travailleur peut terminer la commande en 4 heures, le deuxième 1,25 fois plus rapidement et le troisième en 5 heures. Combien d'heures faudra-t-il pour terminer la commande si trois travailleurs travaillent ensemble ? (Arrondissez la réponse à 0,1 heure près.)
829. Deux voitures travaillent pour nettoyer la rue. Le premier d'entre eux peut nettoyer toute la rue en 40 minutes, le second nécessite 75 % du temps du premier. Les deux machines ont commencé à fonctionner en même temps. Après avoir travaillé ensemble pendant 0,25 heure, la deuxième machine a cessé de fonctionner. Combien de temps après la première machine a-t-elle fini de nettoyer la rue ?
830. 1) L'un des côtés du triangle mesure 2,25 cm, le deuxième est 3,5 cm plus grand que le premier et le troisième est 1,25 cm plus petit que le second. Trouvez le périmètre du triangle.
2) L'un des côtés du triangle mesure 4,5 cm, le deuxième est 1,4 cm de moins que le premier et le troisième côté est égal à la moitié de la somme des deux premiers côtés. Quel est le périmètre du triangle ?
831 . 1) La base du triangle mesure 4,5 cm et sa hauteur est inférieure de 1,5 cm. Trouvez l'aire du triangle.
2) La hauteur du triangle est de 4,25 cm et sa base est 3 fois plus grande. Trouvez l'aire du triangle. (Arrondissez la réponse à 0,1 près.)
832. Trouvez l'aire des figures ombrées (Fig. 38).

833. Quelle surface est la plus grande : un rectangle de 5 cm et 4 cm de côté, un carré de 4,5 cm de côté ou un triangle dont la base et la hauteur mesurent chacune 6 cm ?
834. La pièce mesure 8,5 m de long, 5,6 m de large et 2,75 m de haut. La superficie des fenêtres, portes et poêles représente 0,1 de la surface totale des murs de la pièce. Combien de morceaux de papier peint faudra-t-il pour recouvrir cette pièce si un morceau de papier peint mesure 7 m de long et 0,75 m de large ? (Arrondissez la réponse à l’unité la plus proche.)
835. Il est nécessaire d'enduit et de blanchir l'extérieur d'une maison à un étage dont les dimensions sont : longueur 12 m, largeur 8 m et hauteur 4,5 m. La maison a 7 fenêtres mesurant chacune 0,75 m x 1,2 m et 2 portes mesurant chacune 0,75 m x 2,5 m Combien coûteront l'ensemble des travaux si le blanchiment et le plâtrage font 1 m². m coûte 24 kopecks ? (Arrondissez la réponse au rouble le plus proche.)
836. Calculez la surface et le volume de votre pièce. Trouvez les dimensions de la pièce en mesurant.
837. Le jardin a la forme d'un rectangle dont la longueur est de 32 m et la largeur de 10 m. 0,05 de la superficie totale du jardin est semé de carottes et le reste du jardin est planté de pommes de terre. et des oignons, et une superficie 7 fois plus grande que celle des oignons est plantée de pommes de terre. Quelle superficie de terre est plantée individuellement en pommes de terre, oignons et carottes ?
838. Le potager a la forme d'un rectangle dont la longueur est de 30 m et la largeur de 12 m. 0,65 de la superficie totale du potager est planté de pommes de terre, et le reste de carottes et de betteraves, et 84 mètres carrés sont plantés de betteraves. m plus que des carottes. Quelle superficie de terre y-a-t-il séparément pour les pommes de terre, les betteraves et les carottes ?
839. 1) La boîte en forme de cube était recouverte de contreplaqué sur tous ses côtés. Quelle quantité de contreplaqué a été utilisée si le bord du cube mesure 8,2 dm ? (Arrondissez la réponse au 0,1 dm² le plus proche.)
2) Quelle quantité de peinture sera nécessaire pour peindre un cube avec un bord de 28 cm, si pour 1 m². cm, 0,4 g de peinture sera-t-il utilisé ? (Réponse, arrondissez au 0,1 kg le plus proche.)
840. La longueur d'une billette de fonte en forme de parallélépipède rectangle est de 24,5 cm, la largeur de 4,2 cm et la hauteur de 3,8 cm. Combien pèsent 200 billettes de fonte si 1 cube. le dm de fonte pèse 7,8 kg ? (Arrondissez la réponse au kg près.)
841. 1) La longueur d'une boîte (avec couvercle) en forme de parallélépipède rectangle est de 62,4 cm, largeur 40,5 cm, hauteur 30 cm. Combien de mètres carrés de planches ont été utilisés pour fabriquer la boîte, si les planches de rebut s'élèvent à 0,2 de la surface à recouvrir de planches ? (Arrondissez la réponse au 0,1 m² le plus proche)
2) Le fond et les parois latérales de la fosse, qui a la forme d'un parallélépipède rectangle, doivent être recouverts de planches. La longueur de la fosse est de 72,5 m, la largeur de 4,6 m et la hauteur de 2,2 m. Combien de mètres carrés de planches ont été utilisés pour le revêtement si les déchets de planches constituent 0,2 de la surface à gainer de planches ? (Arrondissez la réponse au m² le plus proche)
842. 1) La longueur du sous-sol, en forme de parallélépipède rectangle, est de 20,5 m, la largeur est de 0,6 de sa longueur et la hauteur est de 3,2 m. Le sous-sol a été rempli de pommes de terre à 0,8 de son volume. Combien de tonnes de pommes de terre peuvent contenir dans le sous-sol si 1 mètre cube de pommes de terre pèse 1,5 tonne ? (Réponse ronde au millier près.)
2) La longueur du réservoir, en forme de parallélépipède rectangle, est de 2,5 m, la largeur est de 0,4 de sa longueur et la hauteur est de 1,4 m. Le réservoir est rempli de kérosène à 0,6 de son volume. Combien de tonnes de kérosène sont versées dans le réservoir si le poids du kérosène dans un volume est de 1 mètre cube ? m est égal à 0,9 t ? (Arrondissez la réponse à 0,1 t près.)
843. 1) Combien de temps faut-il pour renouveler l'air dans une pièce de 8,5 m de long, 6 m de large et 3,2 m de haut, si on passe par une fenêtre en 1 seconde. passe 0,1 mètre cube. m d'air ?
2) Calculez le temps nécessaire pour rafraîchir l'air de votre pièce.
844. Les dimensions du bloc de béton pour murs de construction sont les suivantes : 2,7 m x 1,4 m x 0,5 m. Le vide représente 30 % du volume du bloc. Combien de mètres cubes de béton seront nécessaires pour fabriquer 100 de ces blocs ?
845. Niveleuse-élévatrice (machine à creuser des fossés) en 8 heures. Les travaux réalisent un fossé de 30 cm de large, 34 cm de profondeur et 15 km de long. Combien de pelleteuses une telle machine remplace-t-elle si une pelleteuse peut extraire 0,8 mètre cube ? m par heure ? (Arrondissez le résultat.)
846. Le bac en forme de parallélépipède rectangle mesure 12 m de long et 8 m de large. Dans ce bac, le grain est versé jusqu'à une hauteur de 1,5 m. Afin de connaître le poids de tout le grain, ils ont pris une caisse de 0,5 m de long, 0,5 m de large et 0,4 m de haut, l'ont remplie de grain et l'ont pesée. Combien pesait le grain dans le silo si le grain dans la caisse pesait 80 kg ?

848. 1) À l'aide du schéma « Production d'acier en RSFSR » (Fig. 39). répondre aux questions suivantes:

a) De combien de millions de tonnes la production d'acier a-t-elle augmenté en 1959 par rapport à 1945 ?
b) Combien de fois la production d'acier en 1959 était-elle supérieure à la production d'acier en 1913 ? (Précis à 0,1.)
2) A l'aide du schéma « Superficies cultivées en RSFSR » (Fig. 40), répondez aux questions suivantes :

a) De combien de millions d'hectares la superficie cultivée a-t-elle augmenté en 1959 par rapport à 1945 ?
b) Combien de fois la superficie ensemencée en 1959 était-elle supérieure à celle de 1913 ?
849. Construisez un diagramme linéaire de la croissance de la population urbaine en URSS, si en 1913 la population urbaine était de 28,1 millions de personnes, en 1926 - 24,7 millions, en 1939 - 56,1 millions et en 1959 - 99, 8 millions de personnes.
850. 1) Faites un devis pour la rénovation de votre classe, si vous devez blanchir les murs et le plafond, et peindre le sol. Renseignez-vous auprès du gardien de l'école pour établir un devis (taille des classes, coût du blanchiment à la chaux 1 m², coût de la peinture du sol 1 m²).
2) Pour planter dans le jardin, l'école a acheté des plants : 30 pommiers pour 0,65 roubles. par pièce, 50 cerises pour 0,4 roubles. par pièce, 40 groseilliers pour 0,2 roubles. et 100 framboisiers pour 0,03 roubles. pour un buisson. Rédigez une facture pour cet achat en utilisant l'exemple suivant :

Organisation : École secondaire MBOU Bestuzhevskaya
Localité: s. Bestuzhevo, district d'Ustyansky, région d'Arkhangelsk
Matériel didactique sur le sujet :
« Décimales. Opérations avec des fractions décimales. Intérêt"
« Le matériel didactique est un type particulier de support pédagogique visuel (principalement des cartes, des tableaux, des jeux de cartes avec du texte, des chiffres ou des images, etc.), distribué aux étudiants pour un travail autonome en classe ou à la maison. Les collections de tâches et d'exercices sont également appelées matériel didactique.
- Ce matériel didactique a été développé sur le thème : « Fractions décimales. Opérations avec des fractions décimales. Intérêt." est conçu pour les élèves de 5e année du secondaire et est destiné à la formation et au développement de la culture informatique des élèves sur ce sujet.
Cible de ce matériel didactique – la maîtrise des compétences informatiques des étudiants dans le travail avec les décimales et les pourcentages ; développement de l'activité cognitive et augmentation de la motivation éducative chez les élèves de cinquième année ; développer une culture de l'activité d'apprentissage chez les élèves et accroître l'intérêt pour les mathématiques.
Tâches:
1) Former et développer des compétences informatiques pour travailler avec des décimales et des pourcentages chez les élèves de cinquième année lors de la résolution des tâches de ce matériel didactique ;
2) Augmenter la motivation éducative et l'intérêt pour l'étude des mathématiques chez les étudiants en résolvant des tâches non standard du matériel didactique ;
3) Développer l'activité cognitive et une culture de l'activité éducative des étudiants sous diverses formes de travail avec ce matériel didactique.
Ce matériel didactique se présente sous forme de fiches avec diverses tâches non standards. Le premier type de tâches concerne les mots croisés numériques. Dans ces mots croisés, la réponse peut être un nombre entier ou un nombre décimal fini. De tels mots croisés sont une alternative aux exemples tirés des manuels scolaires. Lorsque vous résolvez des mots croisés, vous devez effectuer une opération avec des fractions décimales, écrire la réponse dans les mots croisés et garder à l'esprit que chaque caractère est écrit dans une cellule distincte. À la fin de chaque carte de mots croisés se trouvent des instructions sur la façon de remplir les réponses. En résolvant de tels mots croisés numériques, les élèves peuvent contrôler l'exactitude de leurs solutions (lorsqu'ils travaillent individuellement avec des mots croisés) ou se contrôler mutuellement (lorsqu'ils travaillent en paires ou en petits groupes). Les mots croisés du matériel didactique sont présentés sur les thèmes suivants : « Écrire des nombres décimaux », « Additionner et soustraire des nombres décimaux », « Multiplier des nombres décimaux par un nombre naturel », « Diviser des nombres décimaux par un nombre naturel », « Multiplier des nombres décimaux », « Diviser un nombre »à une décimale."
Le matériel didactique contient également des tâches dont la réponse peut être un mot, une phrase, un dicton ou le nom d'un scientifique. Dans de telles tâches, l'étudiant résout un exemple et reçoit une réponse qui correspond à une lettre spécifique. En résolvant tous les exemples de la tâche, vous pouvez obtenir un terme dont la signification est donnée ci-dessous ; un proverbe ou le nom d'un scientifique qui a contribué au développement des mathématiques. En résolvant de telles tâches, les élèves apprendront des faits intéressants sur l’histoire des mathématiques, sur divers appareils de comptage anciens et sur l’histoire qui les intéresse. Dans le processus de résolution de tâches, les élèves peuvent contrôler eux-mêmes l'exactitude de leurs décisions ou l'enseignant peut les contrôler. À la fin de la fiche de tâche se trouvent des instructions pour remplir les réponses. Ces tâches sont de nature pédagogique et visent à élargir les horizons des étudiants. Le matériel didactique contient des tâches sur les thèmes : « Addition et soustraction de nombres décimaux », « Multiplication de nombres décimaux par un nombre naturel », « Multiplication et division de nombres décimaux par un nombre naturel », « Multiplication de nombres décimaux », « Multiplication et division de nombres décimaux », « Tous opérations avec des fractions décimales », « Moyenne arithmétique », « Trouver un nombre par son pourcentage ».
Ce matériel didactique contient des tâches dans lesquelles vous devez insérer des nombres manquants. Il s'agit d'une chaîne de calculs dans laquelle un nombre est donné : le premier, le dernier ou le nombre au milieu de la chaîne, et vous devez disposer les nombres restants, en effectuant des actions dans un sens ou dans l'autre. Les chaînes de calculs sont présentées dans différents niveaux de complexité. Cela inclut également les tâches dans lesquelles vous devez insérer les nombres manquants dans un cercle, en effectuant diverses actions avec le nombre au centre. De telles tâches nécessitent un contrôle et une vérification par l'enseignant et sont conçues pour des calculs oraux ou de petits travaux de test. Ces tâches sont présentées sur les thèmes : « Additionner et soustraire des nombres décimaux », « Multiplier et diviser des nombres décimaux par des nombres naturels », « Actions avec des décimales », « Pourcentages ».
Le prochain type de tâches contenues dans le matériel didactique sont les tâches permettant de déterminer la vérité ou la fausseté d'un énoncé, qui sont également conçues pour une solution orale ou une dictée mathématique. Dans de telles tâches, une déclaration est donnée ou un exemple est résolu et vous devez déterminer si elle est vraie ou fausse et mettre « I » ou « L » dans le cercle à côté de la déclaration. Lors de la résolution de telles tâches, les étudiants doivent être supervisés par l'enseignant. Les tâches sont présentées sur les thèmes suivants : « Lire et écrire des fractions décimales », « Multiplier un nombre par 0,1 ; 0,01 ; 0,001 ; …….”
Le dernier type de tâches de ce matériel didactique sont les tâches permettant de trouver des erreurs dans des exemples ou dans la résolution d'équations. Dans de telles tâches, vous devez rechercher et corriger les erreurs proposées ; chaque carte avec une tâche de maîtrise de soi indique le nombre d'erreurs commises. La tâche est vérifiée par l'enseignant. Les tâches sont présentées sur les thèmes : « Diviser des fractions décimales par un nombre naturel », « Diviser un nombre par 0,1 ; 0,01 ; 0,001 ; ….. »
En utilisant des tâches non standard de ce matériel didactique, les étudiants développent une culture informatique, développent et mettent en pratique des compétences informatiques sur le thème : « Décimales. Opérations avec des fractions décimales. Intérêt." Les tâches du matériel didactique aident à susciter chez les élèves un intérêt pour les mathématiques, à augmenter leur activité cognitive et leur motivation à apprendre. À l'aide de matériel didactique, les élèves de cinquième année développent la capacité de comprendre et d'assimiler de manière indépendante du matériel sur un sujet donné et développent leur ingéniosité. Ce matériel didactique peut être utilisé dans les cours pour permettre aux étudiants de travailler individuellement, en binôme ou en petits groupes. Pour le travail individuel, les devoirs sont confiés aux étudiants les plus forts, les plus faibles travaillent en binôme ou en groupe de 3-4 personnes. Ces tâches sont évaluées de différentes manières : auto-évaluation par les étudiants, évaluation mutuelle lors du travail en binôme ou en groupe, évaluation du travail par l'enseignant. Les devoirs de matériel didactique peuvent être utilisés pour les devoirs et l'auto-préparation des étudiants. Le matériel didactique peut être utilisé à différentes étapes de la leçon. Au stade de la mise à jour des connaissances, des chaînes de calculs et de tâches sont utilisées pour déterminer la vérité et la fausseté des affirmations, et ces tâches peuvent également être utilisées lors de la réalisation de dictées mathématiques. Des mots croisés numériques et des tâches de mots, d'expressions ou de noms scientifiques peuvent être utilisés pendant les phases de consolidation et d'application. Ce matériel didactique peut être utilisé pour contrôler et tester les connaissances des étudiants sur le thème : « Fractions décimales. Opérations avec des fractions décimales. Intérêt." En résolvant ce type de tâches, les étudiants développent une culture de l'activité d'apprentissage : s'il s'agit d'un travail individuel, alors l'étudiant détermine de manière indépendante les étapes à résoudre et peut se contrôler et s'évaluer, et peut faire preuve d'ingéniosité ; s'il s'agit d'un travail en binôme ou en petit groupe, les élèves se répartissent les tâches, se contrôlent et procèdent à une évaluation mutuelle. Le matériel didactique vise la maîtrise de soi de la part des étudiants, le contrôle mutuel et la formation au processus de maîtrise du matériel pédagogique. Lorsqu'il travaille avec du matériel didactique, l'étudiant résout un problème didactique spécifique en utilisant ses connaissances et ses compétences, tout en développant ses sphères intellectuelle, motivationnelle, volitive et émotionnelle. D'après l'expérience de l'utilisation de ce matériel didactique, je peux dire que les étudiants acceptent ces tâches avec brio et aiment particulièrement résoudre des mots croisés numériques.
Lorsqu'ils utilisent ce matériel didactique dans le processus d'apprentissage, les étudiants forment tous les groupes d'UUD (activités d'apprentissage universelles). L'UUD est un ensemble de méthodes d'action d'un étudiant (ainsi que des compétences d'apprentissage associées), garantissant sa capacité à acquérir de manière autonome de nouvelles connaissances et compétences, y compris l'organisation de ce processus. Formé et développé :
UUD personnelle– utilisation des connaissances acquises, motivation à apprendre, évaluation de ses propres activités éducatives.
UUD réglementaire- organisation et planification de ses activités éducatives, analyse indépendante des conditions d'atteinte de l'objectif, prévision et anticipation du résultat, contrôle et correction de ses activités.
UUD cognitive - structurer les connaissances, choisir les moyens les plus efficaces pour résoudre des problèmes en fonction de conditions spécifiques, maîtriser l'analyse et la synthèse, rechercher et isoler les informations nécessaires.
UUD communicative - la capacité de formuler des pensées, de planifier la coopération éducative avec l'enseignant et les pairs, de gérer le comportement du partenaire - contrôle, correction, évaluation des actions du partenaire, la capacité de défendre son point de vue.
Ce matériel didactique a été développé sur la base de manuels de mathématiques pour la 5e année : « Mathématiques 5 » par l'équipe d'auteurs Vilenkin N. Ya., Zhokhov V. I., Chesnokov A. S., Shvartsburd S. I., ainsi que « Mathématiques 5 » par les auteurs de l'équipe Merzlyak A. G. , Polonsky V. B., Yakir M. S. Les tâches du matériel didactique peuvent être utilisées par les enseignants dans le processus d'enseignement des mathématiques en 5e année à l'aide de manuels d'autres auteurs. En outre, le matériel didactique constituera un bon assistant dans l’auto-préparation des étudiants. A la fin du matériel didactique, les réponses aux devoirs sont fournies.
Bibliographie:
1. Vilenkin N. Ya., Zhokhov V. I., Chesnokov A. S., Shvartsburd S. I. Mathématiques 5e, 6e année, manuel Moscou Mnemosyne, 2013.
2. Glazer G.I. Histoire des mathématiques à l'école. M. : Éducation, 1981.
3. Merzlyak A. G., Polonsky V. B., Yakir M. S. Mathématiques 5, 6 années. Moscou Ventana-Graf, 2013.
4. Merzlyak A. G., Polonsky V. B., Rabinovich E. M., Yakir M. S.. Matériel didactique. Mathématiques 5e, 6e année. Moscou Ventana-Graf, 2015.
5. Rapatsevich E. S. Le dernier dictionnaire psychologique et pédagogique. Ecole moderne, 2010.
6. Le noyau fondamental du contenu de l'enseignement général, édité par Kozlov V.V., Kondakov A.M.M. : Education 2011.
7. Chesnokov A. S., Neshkov K. I. Matériel didactique en mathématiques 5e, 6e année. Style classique de Moscou, 2010.
8. Wikipédia. Encyclopédie gratuite. https://ru.wikipedia.org/wiki/
Nous consacrerons ce matériel à un sujet aussi important que les fractions décimales. Tout d'abord, définissons les définitions de base, donnons des exemples et attardons-nous sur les règles de la notation décimale, ainsi que sur les chiffres des fractions décimales. Ensuite, nous soulignons les principaux types : fractions finies et infinies, périodiques et non périodiques. Dans la dernière partie, nous montrerons comment les points correspondant aux nombres fractionnaires sont situés sur l'axe des coordonnées.
Yandex.RTB R-A-339285-1
Qu'est-ce que la notation décimale des nombres fractionnaires
La notation dite décimale des nombres fractionnaires peut être utilisée aussi bien pour les nombres naturels que pour les nombres fractionnaires. Cela ressemble à un ensemble de deux nombres ou plus séparés par une virgule.
Le point décimal est nécessaire pour séparer la partie entière de la partie fractionnaire. En règle générale, le dernier chiffre d'une fraction décimale n'est pas un zéro, à moins que le point décimal n'apparaisse immédiatement après le premier zéro.
Quels sont quelques exemples de nombres fractionnaires en notation décimale ? Cela peut être 34, 21, 0, 35035044, 0, 0001, 11 231 552, 9, etc.
Dans certains manuels, vous pouvez trouver l'utilisation d'un point au lieu d'une virgule (5. 67, 6789. 1011, etc.). Cette option est considérée comme équivalente, mais elle est plus typique pour les sources de langue anglaise.
Définition des décimales
Sur la base du concept de notation décimale ci-dessus, nous pouvons formuler la définition suivante des fractions décimales :
Définition 1
Les décimales représentent des nombres fractionnaires en notation décimale.
Pourquoi devons-nous écrire les fractions sous cette forme ? Cela nous donne certains avantages par rapport aux notations ordinaires, par exemple une notation plus compacte, surtout dans les cas où le dénominateur contient 1000, 100, 10, etc., ou un nombre mixte. Par exemple, au lieu de 6 10, nous pouvons spécifier 0,6, au lieu de 25 10000 - 0,0023, au lieu de 512 3 100 - 512,03.
Comment représenter correctement des fractions ordinaires avec des dizaines, des centaines, des milliers au dénominateur sous forme décimale sera discuté dans un document séparé.
Comment lire correctement les décimales
Il existe quelques règles pour lire les notations décimales. Ainsi, les fractions décimales qui correspondent à leurs équivalents ordinaires réguliers se lisent presque de la même manière, mais avec l'ajout des mots « zéro dixième » au début. Ainsi, l’entrée 0, 14, qui correspond à 14 100, se lit comme « zéro virgule quatorze centièmes ».
Si une fraction décimale peut être associée à un nombre fractionnaire, alors elle se lit de la même manière que ce nombre. Ainsi, si nous avons la fraction 56 002, qui correspond à 56 2 1000, nous lisons cette entrée comme « cinquante-six virgule deux millièmes ».
La signification d'un chiffre dans une fraction décimale dépend de l'endroit où il se trouve (comme dans le cas des nombres naturels). Ainsi, dans la fraction décimale 0,7, sept équivaut à des dixièmes, dans 0,0007 à des dix millièmes et dans la fraction 70 000,345, cela signifie sept dizaines de milliers d'unités entières. Ainsi, dans les fractions décimales, il existe également la notion de valeur de position.
Les noms des chiffres situés avant la virgule décimale sont similaires à ceux qui existent dans les nombres naturels. Les noms de ceux situés après sont clairement présentés dans le tableau :
Regardons un exemple.
Exemple 1
Nous avons la fraction décimale 43 098. Elle a un quatre à la place des dizaines, un trois à la place des unités, un zéro à la place des dixièmes, un 9 à la place des centièmes et un 8 à la place des millièmes.
Il est d'usage de distinguer les rangs des fractions décimales par priorité. Si nous parcourons les nombres de gauche à droite, nous passerons du plus significatif au moins significatif. Il s’avère que les centaines sont plus anciennes que les dizaines et que les parties par million sont plus jeunes que les centièmes. Si nous prenons cette fraction décimale finale que nous avons citée comme exemple ci-dessus, alors la place la plus élevée ou la plus élevée sera la place des centaines, et la place la plus basse ou la plus basse sera la 10 millième.
Toute fraction décimale peut être développée en chiffres individuels, c'est-à-dire présentée sous forme de somme. Cette action s'effectue de la même manière que pour les nombres naturels.
Exemple 2
Essayons de développer la fraction 56, 0455 en chiffres.
Nous allons obtenir:
56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005
Si nous nous souvenons des propriétés d'addition, nous pouvons représenter cette fraction sous d'autres formes, par exemple comme la somme 56 + 0, 0455, ou 56, 0055 + 0, 4, etc.
Que sont les décimales de fin ?
Toutes les fractions dont nous avons parlé ci-dessus sont des décimales finies. Cela signifie que le nombre de chiffres après la virgule est fini. Dérivons la définition :
Définition 1
Les décimales de fin sont un type de fraction décimale qui comporte un nombre fini de décimales après le signe décimal.
Des exemples de telles fractions peuvent être 0, 367, 3, 7, 55, 102567958, 231 032, 49, etc.
Chacune de ces fractions peut être convertie soit en un nombre fractionnaire (si la valeur de sa partie fractionnaire est différente de zéro), soit en une fraction ordinaire (si la partie entière est nulle). Nous avons consacré un article séparé à la façon dont cela se fait. Ici, nous nous contenterons de rappeler quelques exemples : par exemple, nous pouvons réduire la fraction décimale finale 5, 63 à la forme 5 63 100, et 0, 2 correspond à 2 10 (ou toute autre fraction égale, par exemple exemple, 4 20 ou 1 5.)
Mais le processus inverse, c'est-à-dire écrire une fraction commune sous forme décimale n’est pas toujours possible. Ainsi, 5 13 ne peut pas être remplacé par une fraction égale avec le dénominateur 100, 10, etc., ce qui signifie qu'une fraction décimale finale ne peut pas en être obtenue.
Principaux types de fractions décimales infinies : fractions périodiques et non périodiques
Nous avons indiqué ci-dessus que les fractions finies sont ainsi appelées parce qu’elles ont un nombre fini de chiffres après la virgule. Cependant, il se peut qu'elle soit infinie, auquel cas les fractions elles-mêmes seront également appelées infinies.
Définition 2
Les fractions décimales infinies sont celles qui ont un nombre infini de chiffres après la virgule.
De toute évidence, ces nombres ne peuvent tout simplement pas être écrits dans leur intégralité, nous n'en indiquons donc qu'une partie, puis ajoutons des points de suspension. Ce signe indique une continuation infinie de la séquence des décimales. Des exemples de fractions décimales infinies incluent 0, 143346732…, 3, 1415989032…, 153, 0245005…, 2, 66666666666…, 69, 748768152…. etc.
La « queue » d'une telle fraction peut contenir non seulement des séquences de nombres apparemment aléatoires, mais également une répétition constante du même caractère ou groupe de caractères. Les fractions avec des nombres alternés après la virgule décimale sont appelées périodiques.
Définition 3
Les fractions décimales périodiques sont des fractions décimales infinies dans lesquelles un chiffre ou un groupe de plusieurs chiffres est répété après la virgule. La partie répétitive est appelée la période de la fraction.
Par exemple, pour la fraction 3, 444444…. le point sera le chiffre 4, et pour 76, 134134134134... - le groupe 134.
Quel est le nombre minimum de caractères qu’on peut laisser dans la notation d’une fraction périodique ? Pour les fractions périodiques, il suffira d’écrire la période entière une fois entre parenthèses. Donc, fraction 3, 444444…. Il serait correct de l'écrire sous la forme 3, (4) et 76, 134134134134... – sous la forme 76, (134).
En général, les entrées avec plusieurs points entre parenthèses auront exactement la même signification : par exemple, la fraction périodique 0,677777 est la même que 0,6 (7) et 0,6 (77), etc. Les enregistrements de la forme 0, 67777 (7), 0, 67 (7777), etc. sont également acceptables.
Pour éviter les erreurs, nous introduisons une uniformité de notation. Convenons de n'écrire qu'un seul point (la séquence de nombres la plus courte possible), la plus proche de la virgule décimale, et de le mettre entre parenthèses.
Autrement dit, pour la fraction ci-dessus, nous considérerons que l'entrée principale est 0, 6 (7) et, par exemple, dans le cas de la fraction 8, 9134343434, nous écrirons 8, 91 (34).
Si le dénominateur d'une fraction ordinaire contient des facteurs premiers qui ne sont pas égaux à 5 et 2, alors une fois convertis en notation décimale, ils donneront des fractions infinies.
En principe, nous pouvons écrire n’importe quelle fraction finie comme une fraction périodique. Pour ce faire, il suffit d’ajouter un nombre infini de zéros à droite. A quoi ça ressemble en enregistrement ? Disons que nous avons la fraction finale 45, 32. Sous forme périodique, cela ressemblera à 45, 32 (0). Cette action est possible car l’ajout de zéros à droite de toute fraction décimale donne une fraction qui lui est égale.
Une attention particulière doit être portée aux fractions périodiques avec une période de 9, par exemple 4, 89 (9), 31, 6 (9). Il s'agit d'une notation alternative pour les fractions similaires avec une période de 0, elles sont donc souvent remplacées lors de l'écriture par des fractions avec une période nulle. Dans ce cas, un est ajouté à la valeur du chiffre suivant et (0) est indiqué entre parenthèses. L'égalité des nombres résultants peut être facilement vérifiée en les représentant comme des fractions ordinaires.
Par exemple, la fraction 8, 31 (9) peut être remplacée par la fraction correspondante 8, 32 (0). Ou 4, (9) = 5, (0) = 5.
Les fractions périodiques décimales infinies sont classées comme nombres rationnels. En d’autres termes, toute fraction périodique peut être représentée comme une fraction ordinaire, et vice versa.
Il existe également des fractions qui n'ont pas une séquence répétitive sans fin après la virgule. Dans ce cas, on les appelle fractions non périodiques.
Définition 4
Les fractions décimales non périodiques incluent les fractions décimales infinies qui ne contiennent pas de point après la virgule, c'est-à-dire groupe répétitif de nombres.
Parfois, les fractions non périodiques ressemblent beaucoup aux fractions périodiques. Par exemple, 9, 03003000300003... à première vue semble avoir un point, mais une analyse détaillée des décimales confirme qu'il s'agit toujours d'une fraction non périodique. Il faut être très prudent avec de tels chiffres.
Les fractions non périodiques sont classées comme nombres irrationnels. Ils ne sont pas convertis en fractions ordinaires.
Opérations de base avec des décimales
Les opérations suivantes peuvent être effectuées avec des fractions décimales : comparaison, soustraction, addition, division et multiplication. Examinons chacun d'eux séparément.
La comparaison de décimales peut être réduite à la comparaison de fractions qui correspondent aux décimales originales. Mais les fractions infinies non périodiques ne peuvent pas être réduites à cette forme, et la conversion de fractions décimales en fractions ordinaires est souvent une tâche fastidieuse. Comment pouvons-nous effectuer rapidement une action de comparaison si nous devons le faire tout en résolvant un problème ? Il est pratique de comparer des fractions décimales par chiffre de la même manière que nous comparons des nombres naturels. Nous consacrerons un article séparé à cette méthode.
Pour additionner certaines fractions décimales avec d'autres, il est pratique d'utiliser la méthode d'addition de colonnes, comme pour les nombres naturels. Pour ajouter des fractions décimales périodiques, vous devez d'abord les remplacer par des fractions ordinaires et compter selon le schéma standard. Si, selon les conditions du problème, nous devons ajouter des fractions infinies non périodiques, nous devons d'abord les arrondir à un certain chiffre, puis les ajouter. Plus le chiffre auquel nous arrondissons est petit, plus la précision du calcul sera élevée. Pour la soustraction, la multiplication et la division de fractions infinies, un pré-arrondi est également nécessaire.
Trouver la différence entre des fractions décimales est l’inverse de l’addition. Essentiellement, en utilisant la soustraction, nous pouvons trouver un nombre dont la somme avec la fraction que nous soustrayons nous donnera la fraction que nous minimisons. Nous en parlerons plus en détail dans un article séparé.
La multiplication de fractions décimales se fait de la même manière que pour les nombres naturels. La méthode de calcul des colonnes convient également pour cela. On réduit encore cette action avec les fractions périodiques à la multiplication des fractions ordinaires selon les règles déjà étudiées. Les fractions infinies, on s'en souvient, doivent être arrondies avant les calculs.
Le processus de division de nombres décimaux est l’inverse de la multiplication. Lors de la résolution de problèmes, nous utilisons également des calculs en colonnes.
Vous pouvez établir une correspondance exacte entre la fraction décimale finale et un point sur l'axe des coordonnées. Voyons comment marquer un point sur l'axe qui correspondra exactement à la fraction décimale requise.
Nous avons déjà étudié comment construire des points correspondant à des fractions ordinaires, mais les fractions décimales peuvent être réduites à cette forme. Par exemple, la fraction commune 14 10 est la même que 1, 4, donc le point correspondant sera éloigné de l'origine dans le sens positif exactement de la même distance :

Vous pouvez vous passer de remplacer la fraction décimale par une fraction ordinaire, mais utilisez la méthode d'expansion par chiffres comme base. Ainsi, si nous devons marquer un point dont la coordonnée sera égale à 15, 4008, alors nous présenterons d'abord ce nombre comme la somme 15 + 0, 4 +, 0008. Pour commencer, mettons de côté 15 segments unitaires entiers dans le sens positif dès le début du compte à rebours, puis 4 dixièmes d’un segment, puis 8 dix millièmes d’un segment. En conséquence, nous obtenons un point de coordonnées qui correspond à la fraction 15, 4008.
Pour une fraction décimale infinie, il est préférable d'utiliser cette méthode, car elle permet de se rapprocher à volonté du point souhaité. Dans certains cas, il est possible de construire une correspondance exacte à une fraction infinie sur l'axe des coordonnées : par exemple, 2 = 1, 41421. . . , et cette fraction peut être associée à un point du rayon de coordonnées, distant de 0 de la longueur de la diagonale du carré, dont le côté sera égal à un segment unitaire.
Si l'on trouve non pas un point sur l'axe, mais une fraction décimale qui lui correspond, alors cette action est appelée la mesure décimale d'un segment. Voyons comment procéder correctement.
Disons que nous devons passer de zéro à un point donné sur l'axe des coordonnées (ou nous en rapprocher le plus possible dans le cas d'une fraction infinie). Pour ce faire, on reporte progressivement les segments unitaires depuis l'origine jusqu'à arriver au point souhaité. Après des segments entiers, si nécessaire, nous mesurons les dixièmes, les centièmes et les fractions plus petites afin que la correspondance soit la plus précise possible. En conséquence, nous avons reçu une fraction décimale qui correspond à un point donné sur l'axe des coordonnées.
Ci-dessus, nous avons montré un dessin avec le point M. Regardez-le à nouveau : pour en arriver à ce point, il faut mesurer un segment unitaire et quatre dixièmes de celui-ci à partir de zéro, puisque ce point correspond à la fraction décimale 1, 4.
Si nous ne pouvons pas atteindre un point dans le processus de mesure décimale, cela signifie que cela correspond à une fraction décimale infinie.
Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée
Chapitre 2 NOMBRES FRACTIONNELS ET ACTIONS AVEC EUX
§ 45. Problèmes et exemples pour toutes les opérations avec des nombres naturels et des fractions décimales
Premier niveau
1620. Trouver (oralement) :
1) 1,8 + 3,1; 2) 0,05 + 0,18; 3) 4,2 - 1,2;
4) 100 ∙ 0,15; 5) 57 ∙ 0,1; 6) 0,73: 0,1.
1621. Trouver (oralement) :
1) 7,8 + 4,9; 2) 3,7 + 2,51; 3) 1 - 0,6;
4) 2 - 0,17; 5) 0,001 ∙ 29; 6) 4,2: 0,7.
1622. Compter (oralement) :
1) 0,57 + 1,43; 2) 4,27 - 2,07; 3) 4,1 - 2,01;
4) 8 ∙ 1,5; 5) 60: 0,2; 6) 739: 100.
1623. Compter (oralement) :
1) 8,32 ∙ 10; 2) 117,3 ∙ 100; 3) 1,85 ∙ 1000;
4) 3,71 ∙ 0,1; 5) 4,92 ∙ 0,01; 6) 125,3 ∙ 0,001.
1624. Compter (oralement) :
1) 32,7: 10; 2) 45,13: 100; 3) 2792: 1000;
4) 8,3: 0,1; 5) 37,3: 0,01; 6) 13,24: 0,001.
1625. Calculer :
1) 5,18 + 25,37; 2) 0,805 + 7,105;
3) 5,97 + 0,032; 4) 8,91 - 1,328;
5) 71,5 - 16,07; 6) 42 - 7,18.
1626. Calculer :
1) 4,27 + 37,42; 2) 0,913 + 8,39;
3) 4,13 + 0,9027; 4) 4,17 - 0,127;
5) 42,7 - 17,08; 6) 78 - 14,53.
1627. Calculer :
1) 42 ∙ 0,13; 2) 3,6 ∙ 2,5; 3) 7,05 ∙ 800;
4) 15: 4; 5) 72: 2,25; 6) 15,3: 17.
1628. Calculer :
1) 38 ∙ 0,25; 2) 4,8 ∙ 3,5; 3) 4,07 ∙ 900;
4) 18,3: 2; 5) 53,55: 4,25; 6) 406,6: 19.
1629. Écrivez sous forme décimale :
1630. Écrivez sous forme de fraction commune ou de nombre fractionnaire :
1) 2,3; 2) 4,07; 3) 0,23; 4) 10,073.
1631. Comparez :
1) 4,897 et 4,879 ; 2) 7,520 et 7,52 ;
3) 42,57 et 42,572 ; 4) 9,759 et 9,758.
1632. Comparez :
1) 7,896 et 7,869 ; 2) 8.01 et 8.1 ;
3) 47,53 et 47,530 ; 4) 4,571 et 4,578.
Niveau moyen
1633. Calculez 2,5 x + 0,37 si :
1) x = 1,6 ; 2) x = 3,4.
1634. Trouvez la moyenne arithmétique des nombres :
1) 0,573; 1,96; 35,24;
2) 4,82; 89,59; 0,462; 9,368.
1635. Trouvez la moyenne arithmétique des nombres 20,76 ; 80,43 ; 90.24.
1636. En 2,5 heures, le train a parcouru 195 km. Combien de kilomètres le train parcourra-t-il en 3,6 heures s'il roule à la même vitesse ?
1637. Voiture pendant t J'ai roulé pendant des heures à une vitesse de 85 km/h. Écrivez une expression pour trouver la distance parcourue par la voiture et calculez-la si t vaut 0,5 ; 0,8 ; 1.4 ; 3.
1638. Calculez la valeur de l'expression 27,3 - a : b si :
1) une = 33,5 ; b = 2,5 ; 2) une = 32,16 ; b = 13,4.
1639. Résolvez les équations :
1) 12,5 + x = 37,4 ; 2) en + 13,72 = 18,1 ;
3) dans - 137,8 = 27,41 ; 4) 17 - x = 12,42.
1640. Résolvez les équations :
1) 13,7 + a = 18,4 ; 2) x + 13,42 = 18,9 ;
3) b - 142,3 = 15,73 ; 4) 14 - y = 12,142.
1641. Comparez les valeurs :
1) 0,4 m et 4 dm ; 2) 0,2 dm et 20 cm ;
3) 0,07 m et 7 cm ; 4) 0,03 km et 300 m
1642. Comparez les valeurs :
1) 0,2 t et 2 c ; 2) 0,3 c et 31 kg ;
3) 0,8 tonne et 785 kg ; 4) 0,08 kg et 80 g.
1643. La vitesse d'un bateau à moteur en eau calme est de 25,4 km/h et la vitesse du courant fluvial est de 1,8 km/h. Combien de kilomètres le navire parcourt-il ?
1) en 1h30 le long de la rivière ;
2) en 2,4 heures à contre-courant de la rivière ?
1644. Le bateau s'est d'abord déplacé pendant 1,6 heure le long du lac à une vitesse de 25,5 km/h, puis pendant 0,8 heure le long de la rivière à contre-courant. La vitesse actuelle est de 1,7 km/h. Quelle distance le bateau a-t-il parcouru ?
1645. Trouver le sens de l'expression :
1) 15 ∙ (2,7 + 4,2);
2) (5,7 - 2,3) : 4;
3) (5,47 - 4,25) ∙ 10;
4) (4,47 + 2,7) : 10;
5) (13,42 - 4,15) ∙ (12,3 - 0,3);
6) (2,17 + 4,45) : (12,6 - 12,5).
1646. Retrouver le sens de l'expression :
1) (2,43 + 4,15) ∙ 1,7;
2) (12,49 - 3,57) : 0,4;
3) (4,17 - 3,8) ∙ (10,1 - 8,1);
4) (15,7 + 14,9) : (2,91 - 1,21).
1647. Résolvez les équations :
1) 12,5 × = 45 ; 2) dans ∙ 4,8 = 60,6 ;
3) x : 4,7 = 12,3 ; 4) 12,7 : b = 0,01.
1648. Développement d'équations :
1) 3,7 ans = 7,77 ; 2) x ∙ 3,48 = 8,7 ;
3) dans : 5,4 = 13,5 ; 4) 52,54 : x = 3,7.
1649. Composez une expression : de la somme des nombres a et 42,3, soustrayez la différence entre les nombres 15,7 et b . Calculez la valeur de l'expression si a = 3,7 ; b = 2,3.
1650. Sur les 360 élèves de l'école, 40 % ont participé au cross-country. Combien d’élèves ont participé au cross-country ?
1651. Retrouver le sens de l'expression :
1) (120,21 - 37,59) : 34 + 5,43 ∙ 19;
2) (8,57 + 9,585: 4,5) ∙ 3,8 - 42,7: 4.
1652. Retrouver le sens de l'expression :
1) (5,02 - 3,89) ∙ 29 + 0,27: 18;
2) (32,526: 3,9 + 2,26) ∙ 5,4 - 47,2 ∙ 0,5.
1653. Dans quelle mesure la somme des nombres 19,4 et 4,72 est-elle plus grande que la différence de ces mêmes nombres ?
1654. Trouvez la somme de 25,3 dm + 13,7 cm + 15 mm en centimètres.
1655. 32 élèves ont récolté 152 kg de fraises et 33,6 kg de framboises. Combien de kilogrammes de baies chaque élève a-t-il collecté s’il cueillait une quantité égale de chaque type de baie ?
1656. Sur un champ de 420 hectares, il était prévu de collecter 35 centimes de céréales par hectare, mais 1785 tonnes de céréales ont été collectées. De combien de centièmes le rendement par hectare est-il supérieur à celui prévu ?
1657. Trouvez l'aire d'un cube dont l'arête est de 1,5 cm.
1658. Trouvez l'aire et le périmètre d'un carré de 4,7 dm de côté.
1659. Écrivez les fractions par ordre décroissant : 0,27 ; 0,372 ; 0,423 ; 0,279 ; 0,51 ; 0,431 ; 0,307.
1660. Écrivez les fractions par ordre croissant : 4,23 ; 4,32 ; 4,222 ; 43.2 ; 4,232 ; 4.323.
1661. Une corde de 15,3 m de long a été coupée en trois parties. L'un d'eux est cordes, deuxième
plus long que le premier de 1,8 m. Trouvez la longueur de chaque partie.
1662. Le yacht « Trouble » a parcouru 234,9 km en 3 jours de régate. Le premier jour, le yacht a couvertcette distance, et pour le second - 8,3 km de moins que pour le premier. Combien de kilomètres le yacht « Trouble » parcourait-il chaque jour ?
1663. La voiture a parcouru 471 km. Il a parcouru les 205 premiers kilomètres à une vitesse de 82 km/h et le reste à une vitesse de 76 km/h. Combien de temps a-t-il fallu à la voiture pour parcourir toute la distance ?
1664. Le périmètre d'un triangle isocèle est de 15,4 cm. Trouvez sa base si le côté latéral du triangle mesure 5,3 cm.
1665. Trouvez le périmètre d'un triangle isocèle dont la base mesure 4,2 pouces et le côté est 1,5 fois plus grand que la base.
1666. Calculer :
1) (88,57 + 66,87) : 29 - 0,27 ∙ 18;
2) 20,8: (12 - 11,36) - 8: 12,5 + 4,7 ∙ 5,2.
1667. Calculer :
1) (1,37 + 4,86) ∙ 17 - 556,89: 19;
2) (3,81 + 59,427: 9,3) ∙ 7,6 - 10,2 ∙ 4,7.
1668. De combien la somme des nombres 8,1 et 7,2 est-elle supérieure à leur fraction ?
1669. De combien la différence entre les nombres 3,7 et 2,5 est-elle inférieure à leur produit ?
1670. Trouvez la valeur de l'expression a ∙ 2,5 - b si a = 3,6 ; b = 1,117.
1671. Entre quels nombres naturels adjacents est placée la fraction :
1672. Arrondi à :
1) unités : 25,17 ; 37,89 ;
2) dixièmes : 37,893 ; 42.012 ;
3) centièmes : 108,112 ; 213.995.
1673. Arrondi à :
1) unités : 25,372 ; 37,51 ;
2) dixièmes : 13,185 ; 14.002 ;
3) centièmes : 15,894 ; 17 377.
1674. Dessinez un rayon de coordonnées, en prenant 10 cellules comme segment unitaire. Marquez dessus les points A(0,7), B (1,3), C (1), D (0,2), D (1,9).
1675. Dessinez un rayon de coordonnées, en prenant 10 cellules comme segment unitaire. Marquez dessus les points M(0,6), N (1,4), K (0,3), L (2), P (1,8).
1676. Un ours polaire pèse 720 kg et la masse d'un ours brun représente 40 % de la masse d'un ours polaire. Calculez la masse d'un ours brun.
1677. Simplifier l'expression 2.7 x - 0,05 x + 0,75 x et trouvez sa valeur si x = 2,7.
1678. La base d'un triangle isocèle mesure 10,8 cm et la longueur du côté estlongueur de base. Trouvez le périmètre du triangle.
1679. Simplifiez l'expression et calculez son sens :
1) 2,7 a ∙ 2, si a = 3,5 ;
2) 3,2 x ∙ 5y, si x = 0,1 ; dans = 1,7.
1680. Trouver le volume d'un parallélépipède rectangle dont les dimensions sont égales à :
1) 1,2 cm, 5 cm, 1,8 cm ; 2) 1,2 DM, 3 cm, 23 mm.
1681. Exprimez en tonnes et écrivez sous forme décimale :
1) 7 314 kg ; 2) 2 tonnes 511 kg ; 3) 3 cuillères à soupe de 12 kg ; 4) 18 kg.
1682. Exprimez en mètres et écrivez sous forme de fraction décimale :
1) 527 cm ; 2) 12 dm ; 3) 3 m 5 dm ; 4) 5 m 4 cm.336
Assez de niveau
1683. Effectuez la division et arrondissez la fraction résultante :
1) 110 : 57 contre un ; 2) 18 : 7 aux dixièmes ;
3) 15,2 : 0,7 aux centièmes ; 4) 14 : 5,1 aux millièmes.
1684. Effectuez la division et arrondissez la fraction obtenue :
1) 120 : 37 aux dixièmes ; 2) 5,2 : 0,17 aux centièmes.
1685. L'usine a fonctionné pendant 15 jours et a produit en moyenne 45,4 tonnes d'engrais minéraux par jour. Tous les engrais étaient chargés de manière égale dans 25 wagons. Quelle quantité d’engrais a été chargée dans chaque wagon ?
1686. La somme des deux longueurs d'un triangle est de 15 cm, et la longueur du troisième côté représente 80 % de cette somme. Trouvez le périmètre du triangle.
1687. L'un des côtés du rectangle mesure 14,4 cm et la longueur du second est 75 % de la première. Trouvez l'aire et le périmètre de ce rectangle.
1688. Le périmètre d'un triangle est de 36 cm. La longueur d'un des côtés estpérimètre, et la longueur du second est de 40% du périmètre. Trouvez les côtés du triangle.
1689. La longueur d'un parallélépipède rectangle est de 16 dm, la largeur est delongueur et hauteur - 70% de la largeur. Trouvez le volume d'un parallélépipède rectangle.
1690. Trouvez la somme de trois nombres, dont le premier est 4,27 et chacun des suivants est 10 fois plus grand.
1691. La hauteur d'un parallélépipède rectangle est de 16 cm, ce qui estlongueur et 40% de largeur. Trouvez le volume d'un parallélépipède rectangle.
1692. Un côté du rectangle mesure 8,5 cm et le second représente 60 % du premier. Trouvez le périmètre et l'aire du rectangle.
1693. L'un des ouvriers a produit 96 pièces en 6 heures et l'autre 45 pièces en 2,5 heures. Combien d’heures leur faudra-t-il pour produire 119 pièces en travaillant ensemble ?
1694. Qu'est-ce qui est le plus rentable à acheter ?

1695. Qu'est-ce qui est le plus rentable à acheter ?

1696. Composez des problèmes à l'aide de diagrammes et résolvez-les.

1697. Composez des problèmes à l'aide de diagrammes et résolvez-les.

1698. De combien le volume d'un cube augmentera-t-il si son bord passe de 2,5 cm à 3,5 cm ?
1699. Composez une expression numérique et trouvez sa valeur :
1) la différence entre les sommes des nombres 2,72 et 3,82 et
2) le produit de la différence entre les nombres 18,93 et 9,83 et le nombre 10.
17 h 00. Deux cyclistes quittent le village A en direction du village B en même temps à des vitesses de 15,6 km/h et 18,4 km/h. Après 3h30, l'un des cyclistes est arrivé au village B. Combien de kilomètres l'autre cycliste doit-il parcourir ?
1701. Deux voitures quittent la même ville au même moment, dans des directions opposées. La vitesse de l’un d’eux est de 76 km/h, soit 95 % de la vitesse de l’autre. Au bout de combien d’heures la distance entre les voitures sera-t-elle de 390 km ?
1702. Résolvez les équations :
1) 1,17 x + 0,32 x = 3,725 ;
2) 4,7 x - 1,2 x = 4,34 ;
3) 2,47 x - 1,32 x + 1,3 = 4,221 ;
4) 1,4 x + 2,7 x - 8,113 = 2,342.
1703. Résolvez les équations :
1) 4,13 x - 0,17 x = 9,9 ;
2) 5,3 x + 4,8 x - 5,13 = 43,35.
1704. L'angle déplié était divisé par des rayons en bicornes. Le premier estélargi, et le second -d'abord. Trouver les mesures de degré des trois formées coins
1705. Composez des problèmes à l'aide de diagrammes et résolvez-les :

1706. Composez des problèmes à l'aide de diagrammes et résolvez-les :

1707. Résolvez les équations :
1) 2,7(x - 4,7) = 9,45 ; 2) (4,7 + x) : 3,8 = 10,5 ;
3) 2,4 + (x : 3 - 5) = 0,8 ; 4) 2,45 : (2 x - 1,4) = 3,5.
1708. Résolvez les équations :
1) 21 : (4 x + 1,6) = 2,5 ;
2) 3,7 - (x : 2 + 1,5) = 0,8.
1709. Une boule a été fabriquée avec 2,5 g de fil de cuivre dont la masse de 1 m est de 1,2 kg et un morceau de fil de laiton dont la longueur est 8 fois celle du cuivre et dont la masse de 1 m est de 0,2 kg. Quelle quantité d'alliage restera-t-il si la masse de la balle est de 6,4 kg ?
1710. Acheté 2,5 kg de biscuits au prix de 13,6 UAH. par kilogramme et 1,6 kg de bonbons, le prix par kilogramme est 1,5 fois supérieur au prix d'un kilogramme de biscuits. Quelle monnaie devriez-vous obtenir de 100 UAH ?
1711. Remplissez les cellules avec des nombres pour former les exemples corrects :

1712. Remplissez les cellules avec les nombres suivants pour former les exemples corrects :

1713. Le nombre 5,2 est la moyenne arithmétique des nombres 2,1 ; 3.2 et X. Trouvez x.
1714. Trouvez la moyenne arithmétique de quatre nombres, dont le premier est 3,6 et chacun des suivants est 0,2 de plus que le précédent.
1715. Deux motocyclistes partent simultanément d'une ville à l'autre dans la même direction à la vitesse de 72,4 km/h et 67,8 km/h. Après quelle heure la distance entre les motocyclistes sera-t-elle de 11,5 km ?
1716. Le prix de certains produits est de 120 UAH. Combien coûtera ce produit si le prix est :
1) augmenter de 15 % ;
2) réduire de 10 % ;
3) augmenter d'abord de 5 %, puis réduire le nouveau prix de 20 % ?
1717. Trouvez les nombres qui manquent dans la chaîne de calculs :
1718. La voiture a parcouru 170,4 km au cours des deux premières heures et 0,45 de cette distance au cours des heures suivantes. Trouvez la vitesse moyenne de la voiture.
1719. Le train a parcouru 210,5 km au cours des trois premières heures, et 0,6 de cette distance au cours des deux heures suivantes. Trouvez la vitesse moyenne du train.
1720. Le côté d'un triangle équilatéral mesure 11,2 cm. Trouvez le côté d'un carré dont le périmètre est égal au périmètre du triangle.Déterminez l'aire de ce carré.
1721. Trouvez la partie ombrée du cercle :

1722. Trouvez la somme de trois nombres, dont le premier est 37,6, le second estdu premier, et le troisième est la moyenne arithmétique des deux premiers.
1723. Le bateau a parcouru 231 km à contre-courant en 6 heures. Quelle distance parcourra-t-il le long de la rivière en 4 heures si la vitesse actuelle est de 1,4 km/h ?
1724. Deux piétons ont quitté simultanément deux points distants de 8,5 km, dans des directions opposées, en s'éloignant l'un de l'autre. La vitesse de l'un d'eux est de 4,2 km/h, ce qui estvitesse de la seconde. Quelle sera la distance entre les piétons après 2h30 ?
17 h 25. La voiture a roulé pendant 4 heures à une vitesse de 82,5 km/h et 6 heures à une vitesse de 83,7 km/h. Trouvez la vitesse moyenne de la voiture sur tout le parcours.
Haut niveau
1726. Carlson et le Kid ont mangé ensemble 3,6 kg de confiture, et Carlson en a mangé 3 fois plus que le Kid. Quelle quantité de confiture Carlson a-t-il mangée et quelle quantité bébé a-t-il mangée ?
1727. Une charge pesant 4,8 tonnes a été placée sur deux camions, et le premier était chargé de 0,6 tonne de plus que le second. Combien de tonnes de marchandises y a-t-il dans chaque voiture ?
1728. Trois ouvriers, travaillant ensemble, produisirent 1001 pièces en 7 heures. Et le premier faittous les détails, et le second -Tous les détails. Combien de pièces le troisième ouvrier produisait-il par heure ?
1729. Soustrayez 10 % d'un certain nombre et obtenez 48,6. Trouvez ce numéro.
1730. Nous avons ajouté 20 % à un certain nombre et avons obtenu 74,4. Trouvez ce numéro.
1731. Trouvez deux nombres si leur somme est 4,7 et leur différence est 3,1.
1732. La somme de deux nombres est 27,2. Trouvez ces nombres si l’un d’eux est trois fois plus grand que l’autre.
1733. Une corde de 10,6 m de long a été coupée en trois parties. Trouvez leurs longueurs si la troisième partie est 0,4 m plus longue que la première et la deuxième.
1734. La vitesse du bateau est 13 fois supérieure à la vitesse du courant. Se déplaçant au gré du courant pendant 2h30, le bateau a parcouru 63 km. Trouvez la vitesse du bateau et la vitesse du courant.
17 h 35. De deux gares distantes de 385 km, deux trains partaient simultanément l'un vers l'autre et se rencontraient au bout de 2,5 heures. Trouvez les vitesses des trains si l'on sait que la vitesse de l'un d'eux est 1,2 fois la vitesse de l'autre.
1736. La somme de la longueur et de la largeur d'un rectangle est de 9,6 cm, la largeur représentant 60 % de la longueur. Trouvez l'aire et le périmètre du rectangle.
1737. La longueur d'un côté du triangle estpérimètre, et la longueur de l’autre côté estpérimètre. Trouvez les longueurs de ces côtés si le troisième côté mesure 10,4 cm.
1738. L'étudiant a d'abord lu 0,25 du livre entier, puis encore 0,4 du reste, après quoi il s'est avéré que l'étudiant avait lu 30 pages de plus que ce qu'il lui restait à lire. Combien de pages y a-t-il dans le livre ?
1739. Trouver la signification des lettres g, h, m, n, k, l, si :
g : n = 1,8 ; n ∙ k = 1,71 ; h + m = 2,13 ;
k + l = 10,44 ; m ∙ 0,9 = 1,17 ; g - h = 0,79.
1740. EST Trois cartons contiennent ensemble 62,88 kg de marchandises. La première boîte contient 1,4 fois plus de marchandises que la seconde, et la troisième contient autant de marchandises qu'il y en a dans la première et la deuxième combinées. Combien de kilogrammes de marchandises contient chaque carton ?
Exercices à répéter
1741. 1) Suivez ces étapes :

2) Suivez ces étapes :

3) Comparez les nombres indiqués par les chiffres :
1742. 1) Suivez ces étapes :
2) Suivez ces étapes :
2. Trouvez la moyenne arithmétique des nombres 1,8 et 2,6.
A) 1,8 ; B) 2 ; B) 2,6 ; D)2.2.
3. Écrivez le nombre fractionnaire sous forme de fraction décimale
A) 3.13 ; B) 13.3 ; B) 13.003 ; D) 13.03.
4. Après distillation de l'huile, on obtient 30 % de kérosène. Quelle quantité de kérosène obtient-on à partir de 18 tonnes de pétrole ?
A) 6 tonnes ; B) 5,4 tonnes ; B) 54 tonnes ; D) 0,6 t.
5. Le lait constitue 9 % du fromage. Quelle quantité de lait avez-vous bu si vous receviez 36 kg de fromage ?
A) 400 kg ; B) 40 kg ; B) 324 kg ; D) 300 kg.
6. Dans une équipe de basket-ball, deux joueurs ont 19 ans, deux ont 21 ans et un joueur a 26 ans. Quel est l'âge moyen des joueurs de cette équipe ?
A) 19 ans ; B) 21 ans ;
B ) 21,2 ans ; D) 21,4 ans.
7. Lors du séchage, les champignons perdent 89 % de leur masse. Combien de champignons secs obtiendrons-nous avec 60 kg de champignons frais ?
A) 53,4 kg ; B) 6,6 kg ; B) 6 kg ; D) 5,34 kg.
8. Lorsque l'élève a lu 30 % du livre, il a remarqué qu'il lui restait encore 105 pages à lire. Combien de pages y a-t-il dans le livre ?
A) 350 secondes ; B) 250 secondes ; B) 150 secondes ; D) 160s.
9. L'un des opérateurs de saisie informatique a tapé 45 pages de texte en 6 heures et un autre a tapé 26 pages de texte en 4 heures. Combien d’heures leur faudra-t-il pour travailler ensemble pour terminer 35 pages ?
A) 2 heures ; B) 2,5 heures C) 3 heures ; D) 3,5 heures.
10. Une boîte contient des boules blanches et noires, les blanches représentant 30 % de toutes les boules. Combien y a-t-il de boules au total s’il y a 32 boules noires de plus que de boules blanches ?
A) 80 ; B) 70 ; B) 56 ; D) 180.
11. La moyenne arithmétique de deux nombres dont l’un est 4 fois plus grand que l’autre est 6. Trouvez le plus petit de ces deux nombres.
A) 1,5 ; B) 2.4 ; B) 2,5 ; D)9.6.
12. Le prix de certains produits est de 150 UAH. Combien coûtera ce produit si le prix du produit était initialement augmenté de 10 % et que le nouveau prix était ensuite diminué de 15 % ?
A) 142,5 UAH ; B) 157,5 UAH ;
V) 155 UAH ; D) 140,25 UAH.
Tâches de test de connaissances n°9 (§42 - §45)
1. Écrivez sous forme décimale :
1) 15 %; 2) 3 %.
2. Écrivez la fraction décimale sous forme de pourcentage :
1) 0,45; 2) 1,37.
3. Suivez ces étapes :
1) 3,7 + 13,42; 2) 15,8 - 13,12;
3) 4,2 ∙ 2,05; 4) 8,64: 2,4.
4. Sur les 1 200 élèves de l'école, 65 % ont participé à la compétition sportive. Combien d’élèves ont participé à la compétition sportive ?
5. Sergei a acheté un livre pour 8 UAH, soit 40 % de l'argent dont il disposait. Combien de hryvnia Sergei possédait-il ?
6. Trouvez la moyenne arithmétique des nombres 48,5 ; 58,2 ; 46,8 ; 42.2.
7. L'ouvrier a produit 320 pièces. Dans la première heure - 35% de toutes les pièces, la seconde - 40% et la troisième - le reste. Combien de pièces l’ouvrier a-t-il produites au cours de la troisième heure ?
8. La voiture a roulé pendant 2 heures à une vitesse de 66,7 km/h et pendant 3 heures à une vitesse de 72,8 km/h. Trouvez sa vitesse moyenne sur tout le trajet.
9. Le touriste a parcouru 56 km en trois jours. Le premier jour, il a parcouru 30 % de la totalité du trajet, soit 80 % de la distance parcourue par le touriste le deuxième jour. Combien de kilomètres le touriste a-t-il parcouru le troisième jour ?
10. Tâche supplémentaire. La longueur d'un parallélépipède rectangle est de 8,5 cm, soit 2,5 fois supérieure à la largeur et 5,1 cm supérieure à la hauteur. Trouvez le volume de ce parallélépipède rectangle.
11. Tâche supplémentaire. La moyenne arithmétique de deux nombres est de 12,4 et la moyenne arithmétique des huit autres nombres est de 10,7. Trouvez la moyenne arithmétique de ces dix nombres.
§ 31. Problèmes et exemples pour toutes les opérations avec des fractions décimales.
Suivez ces étapes:

767. Trouvez le quotient de division :

772. Calculer:
Trouver X , Si:

776. Le nombre inconnu a été multiplié par la différence entre les nombres 1 et 0,57 et le produit était 3,44. Trouvez le numéro inconnu.
777. La somme du nombre inconnu et de 0,9 a été multipliée par la différence entre 1 et 0,4 et le produit était de 2,412. Trouvez le numéro inconnu.
778. À l'aide des données du diagramme sur la fonte du fer dans la RSFSR (Fig. 36), créez un problème à résoudre auquel vous devez appliquer les actions d'addition, de soustraction et de division.

779. 1) La longueur du canal de Suez est de 165,8 km, la longueur du canal de Panama est inférieure de 84,7 km à celle du canal de Suez et la longueur du canal mer Blanche-Baltique est supérieure de 145,9 km à celle du canal de Panama. Quelle est la longueur du canal Mer Blanche-Baltique ?
2) Le métro de Moscou (en 1959) a été construit en 5 étapes. La longueur de la première étape du métro est de 11,6 km, la deuxième de 14,9 km, la longueur de la troisième est de 1,1 km inférieure à la longueur de la deuxième étape, la longueur de la quatrième étape est de 9,6 km de plus que la troisième étape , et la longueur de la cinquième étape est de 11,5 km moins la quatrième. Quelle était la longueur du métro de Moscou au début de 1959 ?
780. 1) La plus grande profondeur de l'océan Atlantique est de 8,5 km, la plus grande profondeur de l'océan Pacifique est de 2,3 km supérieure à la profondeur de l'océan Atlantique et la plus grande profondeur de l'océan Arctique est 2 fois inférieure à la plus grande profondeur de l'océan Atlantique. Océan Pacifique. Quelle est la plus grande profondeur de l’océan Arctique ?
2) La voiture Moskvich consomme 9 litres d'essence aux 100 km, la voiture Pobeda consomme 4,5 litres de plus que la Moskvich et la Volga 1,1 fois plus que la Pobeda. Combien d'essence consomme une voiture Volga pour 1 km de trajet ? (Arrondissez la réponse à 0,01 l près.)
781. 1) L'étudiant est allé chez son grand-père pendant les vacances. Il a voyagé en train pendant 8,5 heures et depuis la gare à cheval pendant 1,5 heure. Au total, il a parcouru 440 km. À quelle vitesse l'étudiant voyageait-il sur le chemin de fer s'il montait à cheval à une vitesse de 10 km/h ?
2) Le kolkhozien devait se trouver en un point situé à 134,7 km de son domicile. Il a pris le bus pendant 2,4 heures à une vitesse moyenne de 55 km/h et a parcouru le reste du trajet à pied à une vitesse de 4,5 km/h. Combien de temps a-t-il marché ?
782. 1) Au cours de l'été, un spermophile détruit environ 0,12 centième de pain. Au printemps, les pionniers ont exterminé 1 250 spermophiles sur 37,5 hectares. Combien de pain les écoliers ont-ils économisé pour la ferme collective ? Combien y a-t-il de pain économisé pour 1 hectare ?
2) La ferme collective a calculé qu'en détruisant les gaufres sur une superficie de 15 hectares de terres arables, les écoliers ont économisé 3,6 tonnes de céréales. Combien de spermophiles sont détruits en moyenne par hectare de terre si un gaufre détruit 0,012 tonne de céréales au cours de l'été ?
783. 1) Lors de la mouture du blé en farine, 0,1 de son poids est perdu et lors de la cuisson, une cuisson égale à 0,4 du poids de farine est obtenue. Quelle quantité de pain cuit sera produite à partir de 2,5 tonnes de blé ?
2) La ferme collective a collecté 560 tonnes de graines de tournesol. Quelle quantité d'huile de tournesol sera produite à partir des grains collectés si le poids du grain est 0,7 du poids des graines de tournesol et le poids de l'huile obtenue est 0,25 du poids du grain ?
784. 1) Le rendement en crème du lait est de 0,16 du poids de lait et le rendement en beurre de la crème est de 0,25 du poids de la crème. Quelle quantité de lait (en poids) faut-il pour produire 1 quintal de beurre ?
2) Combien de kilogrammes de cèpes faut-il collecter pour obtenir 1 kg de champignons séchés, s'il reste lors de la préparation au séchage 0,5 du poids, et lors du séchage 0,1 du poids du champignon transformé ?
785. 1) Les terres attribuées à la ferme collective sont utilisées comme suit : 55 % d'entre elles sont occupées par des terres arables, 35 % par des prairies, et le reste des terres d'un montant de 330,2 hectares est affecté au jardin de la ferme collective et à les domaines des kolkhoziens. Combien de terres y a-t-il dans la ferme collective ?
2) La ferme collective a ensemencé 75 % de la superficie totale ensemencée en céréales, 20 % en légumes et le reste en graminées fourragères. Quelle superficie ensemencée aurait la ferme collective si elle ensemençait 60 hectares de graminées fourragères ?
786. 1) Combien de quintaux de graines faudra-t-il pour semer un champ en forme de rectangle de 875 m de long et 640 m de large, si l'on sème 1,5 quintaux de graines pour 1 hectare ?
2) Combien de quintaux de graines faudra-t-il pour semer un champ en forme de rectangle si son périmètre est de 1,6 km ? La largeur du champ est de 300 m. Pour semer 1 hectare, il faut 1,5 quintal de graines.
787. Combien de plaques carrées d'un côté de 0,2 dm peuvent tenir dans un rectangle mesurant 0,4 dm x 10 dm ?
788. La salle de lecture a des dimensions de 9,6 mx 5 mx 4,5 m. Pour combien de places la salle de lecture est-elle conçue si 3 mètres cubes sont nécessaires pour chaque personne ? m d'air ?
789. 1) Quelle surface de prairie un tracteur équipé d'une remorque de quatre faucheuses peut-il tondre en 8 heures, si la largeur de travail de chaque faucheuse est de 1,56 m et la vitesse du tracteur est de 4,5 km/h ? (Le temps d'arrêt n'est pas pris en compte.) (Arrondissez la réponse au 0,1 hectare le plus proche.)
2) La largeur de travail du semoir de légumes tracteur est de 2,8 m. Quelle superficie peut être semée avec ce semoir en 8 heures. travailler à une vitesse de 5 km/h ?
790. 1) Déterminez le rendement d’une charrue tracteur à trois corps en 10 heures. travail, si la vitesse du tracteur est de 5 km par heure, l'adhérence d'un corps est de 35 cm et la perte de temps était de 0,1 du temps total passé. (Arrondissez la réponse au 0,1 hectare le plus proche.)
2) Trouver le rendement d'une charrue tracteur à cinq corps en 6 heures. travail, si la vitesse du tracteur est de 4,5 km par heure, l'adhérence d'un corps est de 30 cm et la perte de temps était de 0,1 du temps total passé. (Arrondissez la réponse au 0,1 hectare le plus proche.)
791. La consommation d'eau par 5 km de trajet pour une locomotive à vapeur d'un train de voyageurs est de 0,75 tonne, le réservoir d'eau du tendre contient 16,5 tonnes d'eau. Combien de kilomètres le train aura-t-il suffisamment d’eau pour parcourir si le réservoir est rempli à 0,9 de sa capacité ?
792. La voie d'évitement ne peut accueillir que 120 wagons de marchandises d'une longueur moyenne de 7,6 m. Combien de wagons de voyageurs à quatre essieux, chacun mesurant 19,2 m de long, peuvent tenir sur cette voie si 24 wagons de marchandises supplémentaires sont placés sur cette voie ?
793. Pour assurer la solidité du remblai ferroviaire, il est recommandé de renforcer les pentes en semant des graminées des champs. Pour chaque mètre carré de remblai, il faut 2,8 g de graines, ce qui coûte 0,25 rouble. pour 1 kg. Combien coûtera le semis de 1,02 hectares de talus si le coût des travaux est 0,4 du coût des semences ? (Arrondissez la réponse au rouble le plus proche.)
794. La briqueterie livrait des briques à la gare. 25 chevaux et 10 camions ont travaillé pour transporter les briques. Chaque cheval transportait 0,7 tonne par voyage et effectuait 4 voyages par jour. Chaque véhicule transportait 2,5 tonnes par trajet et effectuait 15 déplacements par jour. Le transport a duré 4 jours. Combien de briques ont été livrées à la gare si le poids moyen d'une brique est de 3,75 kg ? (Arrondissez la réponse au millier d’unités le plus proche.)
795. Le stock de farine était réparti entre trois boulangeries : la première recevait 0,4 du stock total, la deuxième 0,4 du reste et la troisième boulangerie recevait 1,6 tonne de farine de moins que la première. Quelle quantité de farine a été distribuée au total ?
796. En deuxième année de l'institut, il y a 176 étudiants, en troisième année il y en a 0,875 et en première année il y en a une fois et demie plus qu'en troisième année. Le nombre d'étudiants en première, deuxième et troisième années représentait 0,75 du nombre total d'étudiants de cet institut. Combien d’étudiants y avait-il à l’institut ?
___________
797. Trouvez la moyenne arithmétique :
1) deux nombres : 56,8 et 53,4 ; 705.3 et 707.5 ;
2) trois nombres : 46,5 ; 37,8 et 36 ; 0,84 ; 0,69 et 0,81 ;
3) quatre nombres : 5,48 ; 1,36 ; 3.24 et 2.04.
798. 1) Le matin la température était de 13,6°, à midi de 25,5° et le soir de 15,2°. Calculez la température moyenne pour cette journée.
2) Quelle est la température moyenne pour la semaine, si pendant la semaine le thermomètre indiquait : 21° ; 20,3°; 22,2°; 23,5°; 21,1° ; 22,1° ; 20,8° ?
799. 1) L'équipe de l'école a désherbé 4,2 hectares de betteraves le premier jour, 3,9 hectares le deuxième jour et 4,5 hectares le troisième. Déterminez le rendement moyen de l’équipe par jour.
2) Pour établir le délai standard de fabrication d'une nouvelle pièce, 3 tourneurs ont été fournis. Le premier a produit la pièce en 3,2 minutes, le deuxième en 3,8 minutes et le troisième en 4,1 minutes. Calculez la norme de temps qui a été définie pour la fabrication de la pièce.
800. 1) La moyenne arithmétique de deux nombres est 36,4. L'un de ces nombres est 36,8. Trouvez autre chose.
2) La température de l'air a été mesurée trois fois par jour : le matin, à midi et le soir. Trouvez la température de l'air le matin s'il faisait 28,4° à midi, 18,2° le soir et que la température moyenne du jour est de 20,4°.
801. 1) La voiture a parcouru 98,5 km au cours des deux premières heures et 138 km au cours des trois heures suivantes. Combien de kilomètres une voiture moyenne parcourt-elle par heure ?
2) Un test de capture et de pesée de carpes d'un an a montré que sur 10 carpes, 4 pesaient 0,6 kg, 3 pesaient 0,65 kg, 2 pesaient 0,7 kg et 1 pesait 0,8 kg. Quel est le poids moyen d’une carpe d’un an ?
802. 1) Pour 2 litres de sirop coûte 1,05 roubles. pour 1 litre, ajoutez 8 litres d'eau. Combien coûte 1 litre de l'eau obtenue avec du sirop ?
2) L'hôtesse a acheté une boîte de 0,5 litre de bortsch en conserve pour 36 kopecks. et bouilli avec 1,5 litre d'eau. Combien coûte une assiette de bortsch si son volume est de 0,5 litre ?
803. Travaux de laboratoire « Mesure de la distance entre deux points »,
1er rendez-vous. Mesure avec un ruban à mesurer (ruban à mesurer). La classe est divisée en unités de trois personnes chacune. Accessoires : 5-6 pôles et 8-10 tags.
Avancement des travaux : 1) les points A et B sont marqués et une ligne droite est tracée entre eux (voir tâche 178) ; 2) poser le mètre ruban le long de la ligne droite accrochée et marquer à chaque fois l'extrémité du mètre ruban avec une étiquette. 2ème rendez-vous. Mesure, étapes. La classe est divisée en unités de trois personnes chacune. Chaque élève parcourt la distance de A à B en comptant le nombre de ses pas. En multipliant la longueur moyenne de votre pas par le nombre de pas obtenu, vous trouvez la distance de A à B.
3ème rendez-vous. Mesure à l'oeil. Chaque élève tend la main gauche avec le pouce levé (Fig. 37) et pointe son pouce vers le poteau au point B (un arbre sur la photo) de manière à ce que l'œil gauche (point A), le pouce et le point B soient sur le même ligne droite. Sans changer de position, fermez votre œil gauche et regardez votre pouce avec votre droit. Mesurez le déplacement résultant à l'œil nu et augmentez-le de 10 fois. C'est la distance de A à B.

_________________
804. 1) Selon le recensement de 1959, la population de l'URSS était de 208,8 millions d'habitants et la population rurale était de 9,2 millions de plus que la population urbaine. Combien y avait-il de citadins et de ruraux en URSS en 1959 ?
2) Selon le recensement de 1913, la population de la Russie était de 159,2 millions d'habitants et la population urbaine était inférieure de 103,0 millions à la population rurale. Quelle était la population urbaine et rurale en Russie en 1913 ?
805. 1) La longueur du fil est de 24,5 m. Ce fil a été coupé en deux parties de sorte que la première partie soit 6,8 m plus longue que la seconde. Combien de mètres mesure chaque pièce ?
2) La somme de deux nombres est 100,05. Un nombre est 97,06 de plus que l’autre. Trouvez ces numéros.
806. 1) Il y a 8656,2 tonnes de charbon dans trois entrepôts de charbon, dans le deuxième entrepôt il y a 247,3 tonnes de charbon de plus que dans le premier et dans le troisième il y a 50,8 tonnes de plus que dans le second. Combien de tonnes de charbon y a-t-il dans chaque entrepôt ?
2) La somme de trois nombres est 446,73. Le premier nombre est inférieur au deuxième de 73,17 et supérieur au troisième de 32,22. Trouvez ces numéros.
807. 1) Le bateau s'est déplacé le long de la rivière à une vitesse de 14,5 km par heure et à contre-courant à une vitesse de 9,5 km par heure. Quelle est la vitesse du bateau en eau calme et quelle est la vitesse du courant de la rivière ?
2) Le paquebot a parcouru 85,6 km le long du fleuve en 4 heures, et 46,2 km à contre-courant en 3 heures. Quelle est la vitesse du bateau à vapeur en eau calme et quelle est la vitesse du courant de la rivière ?
_________
808. 1) Deux navires à vapeur ont livré 3 500 tonnes de marchandises et un navire à vapeur a livré 1,5 fois plus de marchandises que l'autre. Quelle quantité de marchandises chaque navire transportait-il ?
2) La superficie de deux pièces est de 37,2 mètres carrés. m La superficie d'une pièce est 2 fois plus grande que l'autre. Quelle est la superficie de chaque pièce ?
809. 1) Depuis deux agglomérations distantes de 32,4 km, un motocycliste et un cycliste se sont dirigés simultanément l'un vers l'autre. Combien de kilomètres chacun d'eux parcourra-t-il avant le rendez-vous si la vitesse du motocycliste est 4 fois celle du cycliste ?
2) Trouvez deux nombres dont la somme est 26,35 et le quotient de la division d'un nombre par l'autre est 7,5.
810. 1) L'usine a envoyé trois types de marchandises d'un poids total de 19,2 tonnes. Le poids du premier type de marchandises était trois fois supérieur au poids du deuxième type de marchandises et le poids du troisième type de marchandises était deux fois moins élevé. comme le poids du premier et du deuxième types de marchandises combinés. Quel est le poids de chaque type de marchandise ?
2) En trois mois, une équipe de mineurs a extrait 52,5 mille tonnes de minerai de fer. En mars, il a été produit 1,3 fois, en février 1,2 fois plus qu'en janvier. Quelle quantité de minerai l’équipage a-t-il extrait chaque mois ?
811. 1) Le gazoduc Saratov-Moscou est plus long de 672 km que le canal de Moscou. Trouvez la longueur des deux structures si la longueur du gazoduc est 6,25 fois supérieure à la longueur du canal de Moscou.
2) La longueur de la rivière Don est 3,934 fois supérieure à la longueur de la rivière Moscou. Trouvez la longueur de chaque rivière si la longueur de la rivière Don est supérieure de 1 467 km à la longueur de la rivière Moscou.
812. 1) La différence entre deux nombres est 5,2 et le quotient d'un nombre divisé par un autre est 5. Trouvez ces nombres.
2) La différence entre deux nombres est de 0,96 et leur quotient est de 1,2. Trouvez ces numéros.
813. 1) Un nombre est 0,3 de moins que l’autre et en représente 0,75. Trouvez ces numéros.
2) Un nombre est 3,9 de plus qu’un autre nombre. Si le plus petit nombre est doublé, ce sera 0,5 du plus grand. Trouvez ces numéros.
814. 1) La ferme collective a semé 2 600 hectares de blé et de seigle. Combien d'hectares de terre ont été ensemencés en blé et combien en seigle, si 0,8 de la superficie ensemencée en blé est égal à 0,5 de la superficie ensemencée en seigle ?
2) La collection de deux garçons totalise 660 timbres. De combien de timbres la collection de chaque garçon est composée si 0,5 des timbres du premier garçon est égal à 0,6 de la collection du deuxième garçon ?
815. Deux étudiants avaient ensemble 5,4 roubles. Après que le premier ait dépensé 0,75 de son argent et le second 0,8 de son argent, il leur restait la même somme d’argent. De combien d’argent disposait chaque élève ?
816. 1) Deux bateaux à vapeur partent l'un vers l'autre de deux ports dont la distance est de 501,9 km. Combien de temps leur faudra-t-il pour se rencontrer si la vitesse du premier navire est de 25,5 km par heure et celle du second de 22,3 km par heure ?
2) Deux trains partent l'un vers l'autre de deux points dont la distance est de 382,2 km. Combien de temps leur faudra-t-il pour se rencontrer si la vitesse moyenne du premier train était de 52,8 km/h et celle du second de 56,4 km/h ?
817. 1) Deux voitures ont quitté deux villes situées à une distance de 462 km en même temps et se sont rencontrées au bout de 3,5 heures. Trouvez la vitesse de chaque voiture si la vitesse de la première était supérieure de 12 km/h à la vitesse de la deuxième voiture.
2) Depuis deux agglomérations distantes de 63 km, un motocycliste et un cycliste sont partis en même temps l'un vers l'autre et se sont rencontrés au bout de 1,2 heure. Trouvez la vitesse du motocycliste si le cycliste roulait à une vitesse inférieure de 27,5 km par heure à la vitesse du motocycliste.
818. L'étudiant a remarqué qu'un train composé d'une locomotive à vapeur et de 40 voitures est passé à côté de lui pendant 35 secondes. Déterminez la vitesse du train par heure si la longueur de la locomotive est de 18,5 m et la longueur du wagon est de 6,2 m. (Donnez la réponse avec une précision de 1 km par heure.)
819. 1) Un cycliste a quitté A pour B à une vitesse moyenne de 12,4 km/h. Après 3 heures 15 minutes. un autre cycliste est parti de B vers lui à une vitesse moyenne de 10,8 km/h. Au bout de combien d'heures et à quelle distance de A se retrouveront-ils si 0,32 la distance entre A et B est de 76 km ?
2) Depuis les villes A et B, distantes de 164,7 km, un camion de la ville A et une voiture de la ville B se sont dirigés l'un vers l'autre. La vitesse du camion est de 36 km et la vitesse de la voiture est de 1,25 fois. plus haut. La voiture particulière est repartie 1,2 heure plus tard que le camion. Au bout de combien de temps et à quelle distance de la ville B la voiture particulière rencontrera-t-elle le camion ?
820. Deux navires ont quitté le même port au même moment et font route dans la même direction. Le premier bateau à vapeur parcourt 37,5 km toutes les 1,5 heures et le deuxième bateau à vapeur parcourt 45 km toutes les 2 heures. Combien de temps faudra-t-il pour que le premier navire soit à 10 km du second ?
821. Un piéton a d'abord quitté un point, et 1h30 après sa sortie, un cycliste est parti dans la même direction. À quelle distance du point le cycliste a-t-il rattrapé le piéton si le piéton marchait à une vitesse de 4,25 km/h et le cycliste roulait à une vitesse de 17 km/h ?
822. Le train a quitté Moscou pour Leningrad à 6 heures. 10 minutes. matin et j'ai marché à une vitesse moyenne de 50 km/h. Plus tard, un avion de passagers a décollé de Moscou à destination de Léningrad et est arrivé à Léningrad en même temps que l'arrivée du train. La vitesse moyenne de l'avion était de 325 km par heure et la distance entre Moscou et Léningrad était de 650 km. Quand l’avion a-t-il décollé de Moscou ?
823. Le bateau à vapeur a parcouru le fleuve pendant 5 heures, et à contre-courant pendant 3 heures et n'a parcouru que 165 km. Combien de kilomètres a-t-il parcouru en aval et combien à contre-courant, si la vitesse du débit de la rivière est de 2,5 km par heure ?
824. Le train a quitté A et doit arriver à B à une certaine heure ; après avoir parcouru la moitié du chemin et parcouru 0,8 km en 1 minute, le train a été arrêté pendant 0,25 heure ; après avoir encore augmenté la vitesse de 100 m pour 1 million, le train est arrivé à l'heure à B. Trouvez la distance entre A et B.
825. De la ferme collective à la ville 23 km. Un facteur a roulé à vélo de la ville à la ferme collective à une vitesse de 12,5 km/h. Quatre heures plus tard, le directeur du kolkhoze est entré en ville à cheval à une vitesse égale à 0,6 de celle du facteur. Combien de temps après son départ le kolkhozien rencontrera-t-il le facteur ?
826. Une voiture a quitté la ville A pour la ville B, à 234 km de A, à une vitesse de 32 km/h. 1h75 plus tard, une deuxième voiture a quitté la ville B en direction de la première, dont la vitesse était 1,225 fois supérieure à la vitesse de la première. Combien d'heures après son départ la deuxième voiture rencontrera-t-elle la première ?
827. 1) Un dactylographe peut retaper un manuscrit en 1,6 heure et un autre en 2,5 heures. Combien de temps faudra-t-il aux deux dactylos pour taper ce manuscrit, en travaillant ensemble ? (Arrondissez la réponse à 0,1 heure près.)
2) La piscine est remplie de deux pompes de puissance différente. La première pompe, fonctionnant seule, peut remplir la piscine en 3,2 heures et la seconde en 4 heures. Combien de temps faudra-t-il pour remplir la piscine si ces pompes fonctionnent simultanément ? (Arrondissez la réponse à 0,1 près.)
828. 1) Une équipe peut finaliser une commande en 8 jours. L'autre a besoin de 0,5 fois pour terminer cette commande. La troisième équipe peut finaliser cette commande en 5 jours. Combien de jours faudra-t-il pour finaliser la totalité de la commande si trois équipes travaillent ensemble ? (Arrondissez la réponse à 0,1 jour près.)
2) Le premier travailleur peut terminer la commande en 4 heures, le deuxième 1,25 fois plus rapidement et le troisième en 5 heures. Combien d'heures faudra-t-il pour terminer la commande si trois travailleurs travaillent ensemble ? (Arrondissez la réponse à 0,1 heure près.)
829. Deux voitures travaillent pour nettoyer la rue. Le premier d'entre eux peut nettoyer toute la rue en 40 minutes, le second nécessite 75 % du temps du premier. Les deux machines ont commencé à fonctionner en même temps. Après avoir travaillé ensemble pendant 0,25 heure, la deuxième machine a cessé de fonctionner. Combien de temps après la première machine a-t-elle fini de nettoyer la rue ?
830. 1) L'un des côtés du triangle mesure 2,25 cm, le deuxième est 3,5 cm plus grand que le premier et le troisième est 1,25 cm plus petit que le second. Trouvez le périmètre du triangle.
2) L'un des côtés du triangle mesure 4,5 cm, le deuxième est 1,4 cm de moins que le premier et le troisième côté est égal à la moitié de la somme des deux premiers côtés. Quel est le périmètre du triangle ?
831 . 1) La base du triangle mesure 4,5 cm et sa hauteur est inférieure de 1,5 cm. Trouvez l'aire du triangle.
2) La hauteur du triangle est de 4,25 cm et sa base est 3 fois plus grande. Trouvez l'aire du triangle. (Arrondissez la réponse à 0,1 près.)
832. Trouvez l'aire des figures ombrées (Fig. 38).
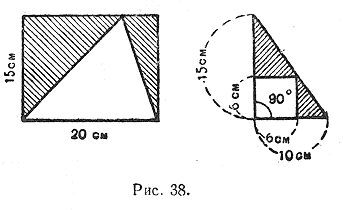
833. Quelle surface est la plus grande : un rectangle de 5 cm et 4 cm de côté, un carré de 4,5 cm de côté ou un triangle dont la base et la hauteur mesurent chacune 6 cm ?
834. La pièce mesure 8,5 m de long, 5,6 m de large et 2,75 m de haut. La superficie des fenêtres, portes et poêles représente 0,1 de la surface totale des murs de la pièce. Combien de morceaux de papier peint faudra-t-il pour recouvrir cette pièce si un morceau de papier peint mesure 7 m de long et 0,75 m de large ? (Arrondissez la réponse à l’unité la plus proche.)
835. Il est nécessaire d'enduit et de blanchir l'extérieur d'une maison à un étage dont les dimensions sont : longueur 12 m, largeur 8 m et hauteur 4,5 m. La maison a 7 fenêtres mesurant chacune 0,75 m x 1,2 m et 2 portes mesurant chacune 0,75 m x 2,5 m Combien coûteront l'ensemble des travaux si le blanchiment et le plâtrage font 1 m². m coûte 24 kopecks ? (Arrondissez la réponse au rouble le plus proche.)
836. Calculez la surface et le volume de votre pièce. Trouvez les dimensions de la pièce en mesurant.
837. Le jardin a la forme d'un rectangle dont la longueur est de 32 m et la largeur de 10 m. 0,05 de la superficie totale du jardin est semé de carottes et le reste du jardin est planté de pommes de terre. et des oignons, et une superficie 7 fois plus grande que celle des oignons est plantée de pommes de terre. Quelle superficie de terre est plantée individuellement en pommes de terre, oignons et carottes ?
838. Le potager a la forme d'un rectangle dont la longueur est de 30 m et la largeur de 12 m. 0,65 de la superficie totale du potager est planté de pommes de terre, et le reste de carottes et de betteraves, et 84 mètres carrés sont plantés de betteraves. m plus que des carottes. Quelle superficie de terre y-a-t-il séparément pour les pommes de terre, les betteraves et les carottes ?
839. 1) La boîte en forme de cube était recouverte de contreplaqué sur tous ses côtés. Quelle quantité de contreplaqué a été utilisée si le bord du cube mesure 8,2 dm ? (Arrondissez la réponse au 0,1 dm² le plus proche.)
2) Quelle quantité de peinture sera nécessaire pour peindre un cube avec un bord de 28 cm, si pour 1 m². cm, 0,4 g de peinture sera-t-il utilisé ? (Réponse, arrondissez au 0,1 kg le plus proche.)
840. La longueur d'une billette de fonte en forme de parallélépipède rectangle est de 24,5 cm, la largeur de 4,2 cm et la hauteur de 3,8 cm. Combien pèsent 200 billettes de fonte si 1 cube. le dm de fonte pèse 7,8 kg ? (Arrondissez la réponse au kg près.)
841. 1) La longueur d'une boîte (avec couvercle) en forme de parallélépipède rectangle est de 62,4 cm, largeur 40,5 cm, hauteur 30 cm. Combien de mètres carrés de planches ont été utilisés pour fabriquer la boîte, si les planches de rebut s'élèvent à 0,2 de la surface à recouvrir de planches ? (Arrondissez la réponse au 0,1 m² le plus proche)
2) Le fond et les parois latérales de la fosse, qui a la forme d'un parallélépipède rectangle, doivent être recouverts de planches. La longueur de la fosse est de 72,5 m, la largeur de 4,6 m et la hauteur de 2,2 m. Combien de mètres carrés de planches ont été utilisés pour le revêtement si les déchets de planches constituent 0,2 de la surface à gainer de planches ? (Arrondissez la réponse au m² le plus proche)
842. 1) La longueur du sous-sol, en forme de parallélépipède rectangle, est de 20,5 m, la largeur est de 0,6 de sa longueur et la hauteur est de 3,2 m. Le sous-sol a été rempli de pommes de terre à 0,8 de son volume. Combien de tonnes de pommes de terre peuvent contenir dans le sous-sol si 1 mètre cube de pommes de terre pèse 1,5 tonne ? (Réponse ronde au millier près.)
2) La longueur du réservoir, en forme de parallélépipède rectangle, est de 2,5 m, la largeur est de 0,4 de sa longueur et la hauteur est de 1,4 m. Le réservoir est rempli de kérosène à 0,6 de son volume. Combien de tonnes de kérosène sont versées dans le réservoir si le poids du kérosène dans un volume est de 1 mètre cube ? m est égal à 0,9 t ? (Arrondissez la réponse à 0,1 t près.)
843. 1) Combien de temps faut-il pour renouveler l'air dans une pièce de 8,5 m de long, 6 m de large et 3,2 m de haut, si on passe par une fenêtre en 1 seconde. passe 0,1 mètre cube. m d'air ?
2) Calculez le temps nécessaire pour rafraîchir l'air de votre pièce.
844. Les dimensions du bloc de béton pour murs de construction sont les suivantes : 2,7 m x 1,4 m x 0,5 m. Le vide représente 30 % du volume du bloc. Combien de mètres cubes de béton seront nécessaires pour fabriquer 100 de ces blocs ?
845. Niveleuse-élévatrice (machine à creuser des fossés) en 8 heures. Les travaux réalisent un fossé de 30 cm de large, 34 cm de profondeur et 15 km de long. Combien de pelleteuses une telle machine remplace-t-elle si une pelleteuse peut extraire 0,8 mètre cube ? m par heure ? (Arrondissez le résultat.)
846. Le bac en forme de parallélépipède rectangle mesure 12 m de long et 8 m de large. Dans ce bac, le grain est versé jusqu'à une hauteur de 1,5 m. Afin de connaître le poids de tout le grain, ils ont pris une caisse de 0,5 m de long, 0,5 m de large et 0,4 m de haut, l'ont remplie de grain et l'ont pesée. Combien pesait le grain dans le silo si le grain dans la caisse pesait 80 kg ?

849. Construisez un diagramme linéaire de la croissance de la population urbaine en URSS, si en 1913 la population urbaine était de 28,1 millions de personnes, en 1926 - 24,7 millions, en 1939 - 56,1 millions et en 1959 - 99, 8 millions de personnes.
850. 1) Faites un devis pour la rénovation de votre classe, si vous devez blanchir les murs et le plafond, et peindre le sol. Renseignez-vous auprès du gardien de l'école pour établir un devis (taille des classes, coût du blanchiment à la chaux 1 m², coût de la peinture du sol 1 m²).
2) Pour planter dans le jardin, l'école a acheté des plants : 30 pommiers pour 0,65 roubles. par pièce, 50 cerises pour 0,4 roubles. par pièce, 40 groseilliers pour 0,2 roubles. et 100 framboisiers pour 0,03 roubles. pour un buisson. Rédigez une facture pour cet achat en utilisant l'exemple suivant :

RÉPONSES











Comment Umar Dzhabrailov a accru puis perdu son influence sur la politique russe
Gafur Rakhimov est devenu le nouveau président de l'AIBA Gafur Akhmedovich Rakhimov est revenu
Biographie du chef James Oliver et de son épouse Juliet Le cinquième enfant de Jamie Oliver est né
Type Coelentérés : caractéristiques générales
Commune de Dacha "Batki" Bokiy Gleb Bokiy 1960 1999 était un homme d'affaires prospère