Tache 1. Le joueur a enregistré ses gains avec un signe + et ses pertes avec un signe –. Trouvez le résultat de chacune des entrées suivantes : a) +7 frotter. +4 frotter.; b) –3 frotter. –6 frotter.; c) –4 frotter. +4 frotter.; d) +8 frotter. –6 roubles ; e) –11 frotter. +7 frotter.; f) +2 frotter. +3 frotter. –5 roubles; g) +6 frotter. –4 frotter. +3 frotter. –5 frotter. +2 frotter. –6 frotter.
L'entrée a) indique que le joueur a d'abord gagné 7 roubles. et puis il a gagné 4 roubles, - au total il a gagné 11 roubles ; l'entrée c) indique que le joueur a d'abord perdu 4 roubles. et puis j'ai gagné 4 roubles - parce que résultat global= 0 (le joueur n'a rien fait) ; l'entrée e) indique que le joueur a d'abord perdu 11 roubles, puis a gagné 7 roubles - la perte dépasse le gain de 4 roubles ; donc, au total, le joueur a perdu 4 roubles. Nous avons donc le droit d'écrire pour ces enregistrements que
a) +7 frotter. +4 frotter. = +11 frotter.; c) –4 frotter. +4 frotter. = 0 ; e) –11 frotter. + 7 frotter. = –4 frotter.
Le reste des entrées est tout aussi facile à comprendre.
Dans leur sens, ces problèmes sont similaires à ceux qui sont résolus en arithmétique en utilisant l'action d'addition, donc ici aussi nous supposerons que partout pour trouver le résultat global du jeu, nous devons additionner des nombres relatifs exprimant les résultats de jeux individuels, par exemple, dans l'exemple c) nombre relatif –11 frotter. s'ajoute au nombre relatif +7 frotter.
Tâche 2. Le caissier enregistrait les encaissements avec le signe + et les dépenses avec le signe –. Trouvez le résultat total de chacune des entrées suivantes : a) +16 frotter. +24 frotter.; b) –17 frotter. –48 frotter.; c) +26 frotter. –26 roubles ; d) –24 frotter. +56 frotter.; e) –24 frotter. +6 frotter.; f) –3 frotter. +25 frotter. –20 frotter. +35 frotter.; g) +17 frotter. –11 frotter. +14 frotter. –9 frotter. –18 roubles. +7 frotter.; h) –9 roubles –7 roubles +15 frotter. –11 frotter. +4 frotter.
Analysons, par exemple, l'entrée f) : comptons d'abord l'intégralité du reçu de caisse : selon cette entrée il y avait 25 roubles. quand j'arrive, et encore 35 roubles. venez, le revenu total était de 60 roubles, et la dépense était de 3 roubles, et encore 20 roubles, le total était de 23 roubles. frais; les revenus dépassent les dépenses de 37 roubles. Piste.,
– 3 frotter. + 25 frotter. – 20 roubles. + 35 frotter. = +37 frotter.
Tâche 3. Le point oscille en ligne droite à partir du point A (Fig. 2).
Merde. 2.
Son déplacement vers la droite est indiqué par un signe + et son déplacement vers la gauche par un signe –. Où sera le point après plusieurs oscillations, enregistrées dans l'une des entrées suivantes : a) +2 dm. –3 dm. +4 points; b) –1 dm. +2 points. +3 points. +4 points. –5 dm. +3 points.; c) +10 dm. –1 dm. +8 points. –2 dm. +6 points. –3 dm. +4 points. –5 dm.; d) –4 dm. +1 points. –6 dm. +3 points. –8 dm. +5 points; e) +5 dm. –6 dm. +8 points. –11 heures. Sur le dessin, les pouces sont indiqués par des segments plus petits que les vrais.
Analysons la dernière entrée (e) : d'abord le point oscillant déplacé vers la droite de A de 5 pouces, puis déplacé vers la gauche de 6 pouces - en général, il doit être situé à gauche de A de 1 pouce, puis déplacé à droite de 8 pouces. , ensuite, il est maintenant à droite de A de 7 pouces, puis déplacé vers la gauche de 11 pouces, donc il est à gauche de A de 4 pouces.
Nous laissons le reste des exemples à l’analyse des étudiants eux-mêmes.
Nous avons accepté que dans tous les enregistrements analysés, nous devions ajouter les nombres relatifs enregistrés. Alors soyons d’accord :
Si plusieurs nombres relatifs sont écrits côte à côte (avec leurs signes), alors ces nombres doivent être additionnés.
Analysons maintenant les principaux cas rencontrés lors de l'addition, et nous prendrons des nombres relatifs sans noms (c'est-à-dire, au lieu de dire, par exemple, 5 roubles pour gagner, et 3 autres roubles pour perdre, ou le point s'est déplacé de 5 pouces vers le à droite de Oh, puis encore 3 pouces vers la gauche, disons 5 unités positives, et aussi 3 unités négatives...).
Ici, vous devez additionner des nombres composés de 8 positions. unités, et même à partir de 5 positions. unités, nous obtenons un nombre composé de 13 positions. unités.
Donc + 8 + 5 = 13
Ici, vous devez ajouter un nombre composé de 6 négatifs. unités avec un nombre composé de 9 négatifs. unités, nous obtenons 15 négatifs. unités (comparez : 6 roubles de perte et 9 roubles de perte - équivaudront à 15 roubles de perte). Donc,
– 6 – 9 = – 15.
4 roubles de gains puis 4 roubles. les pertes, en général, donneront zéro (mutuellement annulées) ; de plus, si un point se déplace de A d'abord vers la droite de 4 pouces, puis vers la gauche de 4 pouces, alors il se retrouvera à nouveau au point A et, par conséquent, sa distance finale à A est nulle, et en général nous devrait supposer que 4 positifs les unités, et même 4 négatives, en général, donneront zéro, ou seront mutuellement détruites. Donc,
4 – 4 = 0, aussi – 6 + 6 = 0, etc.
Deux nombres relatifs qui ont la même valeur absolue, mais divers signes, sont mutuellement détruits.
6 négatif les unités seront détruites à partir de 6 positifs. unités, et il restera encore 3 postes. unités. Donc,
– 6 + 9 = + 3.
7 pos. les unités seront détruites à partir de 7 négatif. unités, et il restera encore 4 négatifs. unités. Donc,
7 – 11 = – 4.
En considérant les cas 1), 2), 4) et 5), nous avons
8 + 5 = + 13 ; – 6 – 9 = – 15 ; – 6 + 9 = + 3 et
+ 7 – 11 = – 4.
On voit de là qu'il faut distinguer deux cas d'addition de nombres algébriques : le cas où les termes ont les mêmes signes (1er et 2ème) et le cas d'addition de nombres avec différents signes(4ème et 5ème).
Ce n'est pas difficile à voir maintenant
lors de l'ajout de nombres avec signes identiques vous devez additionner leurs valeurs absolues et les écrire signe général, et lors de l'addition de deux nombres avec des signes différents, vous devez soustraire arithmétiquement leurs valeurs absolues (du plus grand au plus petit) et écrire le signe du nombre dont valeur absolue plus.
Supposons que nous devions trouver la somme
6 – 7 – 3 + 5 – 4 – 8 + 7 + 9.
Nous pouvons d’abord additionner tous les nombres positifs + 6 + 5 + 7 + 9 = + 27, puis les réduire tous. – 7 – 3 – 4 – 8 = – 22 puis les résultats obtenus entre eux + 27 – 22 = + 5.
On peut aussi utiliser ici le fait que les nombres + 5 – 4 – 8 + 7 s'annulent et il ne reste plus qu'à additionner les nombres + 6 – 7 – 3 + 9 = + 5.
Une autre façon de représenter l'addition
Vous pouvez mettre chaque terme entre parenthèses et écrire un signe d’addition entre parenthèses. Par exemple:
(+7) + (+9); (–3) + (–8); (+7) + (–11); (–4) + (+5);
(–3) + (+5) + (–7) + (+9) + (–11), etc.
On peut, selon la précédente, écrire immédiatement le montant, par exemple. (–4) + (+5) = +1 (cas de l'addition de nombres de signes différents : il faut soustraire le plus petit de la plus grande valeur absolue et écrire le signe du nombre dont la valeur absolue est la plus grande), mais on peut également réécrire d'abord la même chose sans parenthèses, en utilisant notre condition selon laquelle si des nombres sont écrits à côté de leurs signes, alors ces nombres doivent être ajoutés ; piste.,
Pour ouvrir des parenthèses lors de l'ajout de nombres positifs et négatifs, vous devez écrire les termes à côté de leurs signes (omettre le signe d'addition et les parenthèses).
Ex : (+ 7) + (+ 9) = + 7 + 9 ; (– 3) + (– 8) = – 3 – 8 ; (+ 7) + (– 11) = + 7 – 11 ; (– 4) + (+ 5) = – 4 + 5 ; (– 3) + (+ 5) + (– 7) + (+ 9) + (– 11) = – 3 + 5 – 7 + 9 – 11.
Après cela, vous pouvez additionner les nombres obtenus.
Dans un cours d'algèbre, vous devez accorder une attention particulière à la capacité d'ouvrir des parenthèses.
Des exercices.
1) (– 7) + (+ 11) + (– 15) + (+ 8) + (– 1);
>> Mathématiques : Addition de nombres avec des signes différents
33. Ajout de nombres avec des signes différents
Si la température de l'air était égale à 9 °C, puis qu'elle passait à - 6 °C (c'est-à-dire qu'elle diminuait de 6 °C), alors elle devenait égale à 9 + (- 6) degrés (Fig. 83).
Pour additionner les nombres 9 et - 6 à l'aide de , il faut déplacer le point A (9) vers la gauche de 6 segments unitaires (Fig. 84). On obtient le point B (3).
Cela signifie 9+(- 6) = 3. Le nombre 3 a le même signe que le terme 9, et son moduleégal à la différence entre les modules des termes 9 et -6.
En effet, |3| =3 et |9| - |- 6| = = 9 - 6 = 3.
Si la même température de l'air de 9 °C changeait de -12 °C (c'est-à-dire diminuait de 12 °C), elle devenait alors égale à 9 + (-12) degrés (Fig. 85). En additionnant les nombres 9 et -12 à l'aide de la ligne de coordonnées (Fig. 86), nous obtenons 9 + (-12) = -3. Le nombre -3 a le même signe que le terme -12, et son module est égal à la différence entre les modules des termes -12 et 9.
En effet, | - 3| = 3 et | -12| - | -9| =12 - 9 = 3.
Pour additionner deux nombres de signes différents, il faut :
1) soustraire le plus petit du plus grand module des termes ;
2) mettre devant le nombre obtenu le signe du terme dont le module est le plus grand.
Habituellement, le signe de la somme est d'abord déterminé et écrit, puis la différence de modules est trouvée.

Par exemple:
1) 6,1+(- 4,2)= +(6,1 - 4,2)= 1,9,
ou plus court 6,1+(- 4,2) = 6,1 - 4,2 = 1,9 ;

Lorsque vous ajoutez des nombres positifs et négatifs, vous pouvez utiliser micro calculatrice. Entrer un nombre négatif dans le microcalculateur, il faut saisir le module de ce nombre, puis appuyer sur la touche « changement de signe » |/-/|. Par exemple, pour saisir le nombre -56.81, vous devez appuyer séquentiellement sur les touches : | 5 |, | 6 |, | ¦ |, | 8 |, | 1 |, |/-/|. Les opérations sur les nombres de n'importe quel signe sont effectuées sur une microcalculatrice de la même manière que sur les nombres positifs.
Par exemple, la somme -6,1 + 3,8 est calculée en utilisant programme
? Les nombres a et b ont des signes différents. Quel signe aura la somme de ces nombres si le plus grand module est négatif ?
si le plus petit module est négatif ?
si le plus grand module est un nombre positif ?
si le plus petit module est un nombre positif ?
Formulez une règle pour additionner des nombres avec des signes différents. Comment saisir un nombre négatif dans une microcalculatrice ?
À 1045. Le chiffre 6 a été remplacé par -10. De quel côté de l’origine se trouve le nombre obtenu ? A quelle distance de l'origine se trouve-t-il ? A quoi est-il égal somme 6 et -10 ?
1046. Le nombre 10 a été remplacé par -6. De quel côté de l’origine se trouve le nombre obtenu ? A quelle distance de l'origine se trouve-t-il ? Quelle est la somme de 10 et -6 ?
1047. Le nombre -10 a été remplacé par 3. De quel côté de l'origine se trouve le nombre résultant ? A quelle distance de l'origine se trouve-t-il ? Quelle est la somme de -10 et 3 ?
1048. Le nombre -10 a été remplacé par 15. De quel côté de l'origine se trouve le nombre résultant ? A quelle distance de l'origine se trouve-t-il ? Quelle est la somme de -10 et 15 ?
1049. Dans la première moitié de la journée, la température a changé de - 4 °C et dans la seconde moitié de la journée de + 12 °C. De combien de degrés la température a-t-elle changé au cours de la journée ?
1050. Effectuer l'addition :

1051. Ajouter :
a) à la somme de -6 et -12 le nombre 20 ;
b) au nombre 2,6 la somme est de -1,8 et 5,2 ;
c) à la somme -10 et -1,3 la somme de 5 et 8,7 ;
d) à la somme de 11 et -6,5 la somme de -3,2 et -6.
1052. Quel nombre est 8 ; 7.1 ; -7.1 ; -7; -0,5 est la racine équations- 6 + x = -13,1 ?
1053. Devinez la racine de l'équation et vérifiez :
une) x + (-3) = -11 ; c) m + (-12) = 2 ;
b) - 5 + y=15 ; d) 3 + n = -10.
1054. Trouver le sens de l'expression :
1055. Suivez les étapes à l'aide d'une microcalculatrice :
a) - 3,2579 + (-12,308) ; d) -3,8564+ (-0,8397) +7,84 ;
b) 7,8547+ (-9,239) ; e) -0,083 + (-6,378) + 3,9834 ;
c) -0,00154 + 0,0837 ; e) -0,0085+ 0,00354+ (- 0,00921).
P. 1056. Trouver la valeur de la somme :

1057. Trouver le sens de l'expression :
1058. Combien d'entiers se trouvent entre les nombres :
a) 0 et 24 ; b) -12 et -3 ; c) -20 et 7 ?
1059. Imaginez le nombre -10 comme la somme de deux termes négatifs tel que :
a) les deux termes étaient des nombres entiers ;
b) les deux termes étaient des fractions décimales ;
c) l'un des termes était un ordinaire ordinaire fraction.
1060. Quelle est la distance (en segments unitaires) entre les points de la ligne de coordonnées avec les coordonnées :
a) 0 et a ; b) -a et a; c) -a et 0 ; d) a et -Za ?
M 1061. Les rayons des parallèles géographiques de la surface terrestre sur lesquels se trouvent les villes d'Athènes et de Moscou sont respectivement égaux à 5 040 km et 3 580 km (Fig. 87). Dans quelle mesure le parallèle de Moscou est-il plus court que celui d’Athènes ?

1062. Écrivez une équation pour résoudre le problème : « Un champ d'une superficie de 2,4 hectares a été divisé en deux sections. Trouver carré chaque site, s'il est connu que l'un des sites :
a) 0,8 hectare de plus qu'un autre ;
b) 0,2 hectare de moins qu'un autre ;
c) 3 fois plus qu'un autre ;
d) 1,5 fois moins qu'un autre ;
e) en constitue un autre ;
e) est 0,2 de l'autre ;
g) constitue 60 % de l'autre ;
h) représente 140 % de l’autre.
1063. Résolvez le problème :
1) Le premier jour, les voyageurs ont parcouru 240 km, le deuxième jour 140 km, le troisième jour ils ont parcouru 3 fois plus que le deuxième et le quatrième jour ils se sont reposés. Combien de kilomètres ont-ils parcourus le cinquième jour, si sur 5 jours ils ont parcouru en moyenne 230 km par jour ?
2) Le revenu mensuel du père est de 280 roubles. La bourse de ma fille est 4 fois inférieure. Combien gagne une mère par mois s'il y a 4 personnes dans la famille ? fils cadet- un écolier et chaque personne reçoit en moyenne 135 roubles ?
1064. Suivez ces étapes :
1) (2,35 + 4,65) 5,3:(40-2,9);
2) (7,63-5,13) 0,4:(3,17 + 6,83).

1066. Présentez chacun des nombres comme une somme de deux termes égaux :
1067. Trouvez la valeur de a + b si :
une) une= -1,6, b = 3,2 ; b) une=- 2,6, b = 1,9 ; V) ![]()
1068. Il y avait 8 appartements sur un étage d'un immeuble résidentiel. 2 appartements avaient une surface habitable de 22,8 m2, 3 appartements - 16,2 m2, 2 appartements - 34 m2. Quelle surface habitable avait le huitième appartement si à cet étage chaque appartement avait en moyenne 24,7 m2 de surface habitable ?
1069. Le train de marchandises était composé de 42 wagons. Il y avait 1,2 fois plus de wagons couverts que de quais, et le nombre de réservoirs était égal au nombre de quais. Combien de wagons de chaque type y avait-il dans le train ?
1070. Trouver le sens de l'expression 
N.Ya.Vilenkin, A.S. Chesnokov, S.I. Shvartsburd, V.I. Zhokhov, Mathématiques pour la 6e année, Manuel pour lycée
Planification des mathématiques, manuels et livres en ligne, cours et tâches de mathématiques pour la 6e année à télécharger
Contenu de la leçon notes de cours cadre de support présentation de cours méthodes d'accélération technologies interactives Pratique tâches et exercices ateliers d'autotest, formations, cas, quêtes devoirs questions de discussion questions rhétoriques des étudiants Illustrations audio, clips vidéo et multimédia photographies, images, graphiques, tableaux, diagrammes, humour, anecdotes, blagues, bandes dessinées, paraboles, dictons, mots croisés, citations Modules complémentaires résumés articles astuces pour les curieux crèches manuels scolaires dictionnaire de base et supplémentaire des termes autres Améliorer les manuels et les leçonscorriger les erreurs dans le manuel mise à jour d'un fragment dans un manuel, éléments d'innovation dans la leçon, remplacement des connaissances obsolètes par de nouvelles Uniquement pour les enseignants des leçons parfaites plan de calendrier pour un an des lignes directrices programmes de discussion Leçons intégréesPresque tout le cours de mathématiques est basé sur des opérations avec des nombres positifs et négatifs. Après tout, dès que nous commençons à étudier la ligne de coordonnées, des nombres avec des signes plus et moins commencent à nous apparaître partout, dans chaque nouveau sujet. Il n’y a rien de plus simple que d’additionner des nombres positifs ordinaires ; il n’est pas difficile de soustraire l’un de l’autre. Même opérations arithmétiques avec deux nombres négatifs devient rarement un problème.
Cependant, beaucoup de gens ne savent pas ajouter et soustraire des nombres avec des signes différents. Rappelons les règles selon lesquelles ces actions se produisent.
Ajouter des nombres avec des signes différents
Si pour résoudre un problème, nous devons ajouter un nombre négatif « -b » à un nombre « a », alors nous devons agir comme suit.
- Prenons les modules des deux nombres - |a| et |b| - et comparer ces valeurs absolues entre elles.
- Notons quel module est le plus grand et lequel est le plus petit, et soustrayons la plus petite valeur de la plus grande valeur.
- Mettons devant le nombre obtenu le signe du nombre dont le module est le plus grand.
Ce sera la réponse. On peut le dire plus simplement : si dans l'expression a + (-b) le module du nombre « b » est supérieur au module de « a », alors on soustrait « a » de « b » et on met un « moins » devant le résultat. Si le module « a » est supérieur, alors « b » est soustrait de « a » - et la solution est obtenue avec un signe « plus ».
Il arrive aussi que les modules s'avèrent égaux. Si tel est le cas, vous pouvez vous arrêter à ce stade : nous parlons de sur les nombres opposés, et leur somme sera toujours nulle.
Soustraire des nombres avec des signes différents
Nous avons traité de l'addition, regardons maintenant la règle de la soustraction. C'est également assez simple - et en plus, il répète complètement une règle similaire pour soustraire deux nombres négatifs.
Afin de soustraire d'un certain nombre « a » - arbitraire, c'est-à-dire avec n'importe quel signe - un nombre négatif « c », vous devez ajouter à notre nombre arbitraire « a » le nombre opposé à « c ». Par exemple:
- Si « a » est un nombre positif et « c » est négatif et que vous devez soustraire « c » de « a », alors nous l'écrivons comme ceci : a – (-c) = a + c.
- Si « a » est un nombre négatif, que « c » est positif et que « c » doit être soustrait de « a », alors nous l'écrivons comme suit : (- a)– c = - a+ (-c).
Ainsi, lorsqu’on soustrait des nombres de signes différents, on finit par revenir aux règles d’addition, et lorsqu’on additionne des nombres de signes différents, on revient aux règles de soustraction. La mémorisation de ces règles vous permet de résoudre les problèmes rapidement et facilement.
Dans cette leçon, nous apprendrons ce qu’est un nombre négatif et quels nombres sont appelés opposés. Nous apprendrons également comment additionner des nombres négatifs et positifs (des nombres avec des signes différents) et examinerons plusieurs exemples d'addition de nombres avec des signes différents.
Regardez cet équipement (voir Fig. 1).
Riz. 1. Équipement d'horlogerie
Il ne s'agit pas d'une aiguille qui indique directement l'heure ni d'un cadran (voir Fig. 2). Mais sans cette pièce, l’horloge ne fonctionne pas.

Riz. 2. Équipement à l’intérieur de l’horloge
Que représente la lettre Y ? Rien que le son Y. Mais sans cela, de nombreux mots ne « fonctionneront » pas. Par exemple, le mot « souris ». Il en va de même pour les nombres négatifs : ils ne montrent aucune quantité, mais sans eux, le mécanisme de calcul serait beaucoup plus difficile.
Nous savons que l’addition et la soustraction sont des opérations équivalentes et peuvent être effectuées dans n’importe quel ordre. Dans l’ordre direct, nous pouvons calculer : , mais nous ne pouvons pas commencer par soustraction, car nous ne sommes pas encore d’accord sur quoi .
Il est clair qu’augmenter le nombre de puis diminuer signifie finalement diminuer de trois. Pourquoi ne pas désigner cet objet et compter ainsi : ajouter, c'est soustraire. Alors .
Le chiffre peut signifier, par exemple, une pomme. Le nouveau nombre ne représente aucune quantité réelle. En soi, cela ne signifie rien comme la lettre Y. C'est juste un nouvel outil pour faciliter les calculs.
Nommons de nouveaux numéros négatif. Nous pouvons maintenant soustraire le plus grand nombre du plus petit nombre. Techniquement, vous devez toujours soustraire le plus petit nombre du plus grand nombre, mais mettez un signe moins dans votre réponse : .
Regardons un autre exemple : ![]() . Vous pouvez effectuer toutes les actions à la suite : .
. Vous pouvez effectuer toutes les actions à la suite : .
Cependant, il est plus facile de soustraire le troisième nombre du premier nombre puis d’ajouter le deuxième nombre :
Les nombres négatifs peuvent être définis d'une autre manière.
Pour chaque nombre naturel, par exemple , on introduit un nouveau nombre, que l'on note , et on détermine qu'il a la propriété suivante : la somme du nombre et est égale à : .
Nous appellerons le nombre négatif, et les nombres et - ci-contre. Ainsi, nous obtenons un nombre infini de nouveaux nombres, par exemple :
Le contraire du nombre ;
Le contraire du nombre ;
Le contraire du nombre ; ![]()
Le contraire du nombre ;
Soustrayez le plus grand nombre du plus petit nombre : . Ajoutons à cette expression : . Nous avons obtenu zéro. Cependant, selon la propriété : le nombre qui ajoute zéro à cinq est noté moins cinq : . Par conséquent, l’expression peut être notée .
Tout nombre positif possède un nombre jumeau, qui ne diffère que par le fait qu'il est précédé du signe moins. De tels nombres sont appelés opposé(voir fig. 3).

Riz. 3. Exemples de nombres opposés
Propriétés des nombres opposés
1. La somme des nombres opposés est nulle : .
2. Si vous soustrayez un nombre positif de zéro, le résultat sera le nombre négatif opposé : .
1. Les deux nombres peuvent être positifs, et nous savons déjà comment les additionner : .
2. Les deux nombres peuvent être négatifs.
Nous avons déjà abordé l'ajout de nombres comme ceux-ci dans la leçon précédente, mais assurons-nous de bien comprendre quoi en faire. Par exemple: .
Pour trouver cette somme, additionnez les nombres positifs opposés et mettez un signe moins.
3. Un nombre peut être positif et l’autre négatif.
Si cela nous convient, nous pouvons remplacer l'addition d'un nombre négatif par la soustraction d'un nombre positif : .
Encore un exemple : . Encore une fois, nous écrivons le montant comme la différence. Vous pouvez soustraire un nombre plus grand d’un nombre plus petit en soustrayant un nombre plus petit d’un nombre plus grand, mais en utilisant le signe moins.
On peut échanger les termes : .
Autre exemple similaire : .
Dans tous les cas, le résultat est une soustraction.
Pour formuler brièvement ces règles, rappelons encore un terme. Bien entendu, les nombres opposés ne sont pas égaux. Mais il serait étrange de ne pas remarquer ce qu’ils ont en commun. Nous appelons cela commun numéro de module. Le module des nombres opposés est le même : pour un nombre positif il est égal au nombre lui-même, et pour un nombre négatif il est égal à son contraire, positif. Par exemple: , .
Pour ajouter deux nombres négatifs, vous devez additionner leurs modules et mettre un signe moins :
Pour ajouter un nombre négatif et un nombre positif, vous devez soustraire le plus petit module du plus grand module et mettre le signe du nombre avec le plus grand module :
Les deux nombres sont négatifs, nous ajoutons donc leurs modules et mettons un signe moins :
Deux nombres avec des signes différents, donc du module du nombre (le plus grand module), on soustrait le module du nombre et on met un signe moins (le signe du nombre avec le plus grand module) :
Deux nombres de signes différents, donc du module du nombre (le plus grand module), on soustrait le module du nombre et on met un signe moins (le signe du nombre avec le plus grand module) : .
Deux nombres de signes différents, donc du module du nombre (le plus grand module), on soustrait le module du nombre et on met un signe plus (le signe du nombre avec le plus grand module) : .
Les nombres positifs et négatifs ont historiquement joué des rôles différents.
Nous sommes d'abord entrés entiers pour compter les objets :
Ensuite, nous avons introduit d'autres nombres positifs - des fractions, pour compter des quantités non entières, des parties : .
Les nombres négatifs sont apparus comme un outil pour simplifier les calculs. Ce n’était pas comme s’il existait des quantités dans la vie que nous ne pouvions pas compter, et nous avons inventé les nombres négatifs.
Autrement dit, les nombres négatifs ne proviennent pas de monde réel. Ils se sont révélés si pratiques que, dans certains endroits, ils ont trouvé une application dans la vie. Par exemple, on entend souvent parler de températures négatives. Cependant, nous ne rencontrons jamais un nombre négatif de pommes. Quelle est la différence?
La différence est que dans la vie, les quantités négatives ne sont utilisées qu’à des fins de comparaison, mais pas pour les quantités. Si un hôtel dispose d'un sous-sol et qu'un ascenseur y est installé, alors afin de maintenir la numérotation habituelle des étages réguliers, un premier étage négatif peut apparaître. Ce premier moins signifie seulement un étage sous le niveau du sol (voir Fig. 1).

Riz. 4. Moins le premier et moins le deuxième étage
Une température négative n’est négative que par rapport au zéro, choisi par l’auteur de l’échelle, Anders Celsius. Il existe d'autres échelles, et la même température peut n'y être plus négative.
En même temps, on comprend qu'il est impossible de changer le point de départ pour qu'il n'y ait pas cinq pommes, mais six. Ainsi, dans la vie, les nombres positifs servent à déterminer des quantités (pommes, gâteau).
Nous les utilisons également à la place des noms. Chaque téléphone pourrait recevoir son propre nom, mais le nombre de noms est limité et il n'y a pas de numéros. C'est pourquoi nous utilisons des numéros de téléphone. Également pour commander (siècle après siècle).
Les nombres négatifs dans la vie sont utilisés dans ce dernier sens (moins le premier étage en dessous du zéro et le premier étage)
- Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S., Shvartsburd S.I. Mathématiques 6. M. : Mnémosyne, 2012.
- Merzlyak A.G., Polonsky V.V., Yakir M.S. Mathématiques 6ème année. "Gymnase", 2006.
- Depman I.Ya., Vilenkin N.Ya. Derrière les pages d'un manuel de mathématiques. M. : Éducation, 1989.
- Rurukin A.N., Tchaïkovski I.V. Devoirs pour le cours de mathématiques pour les classes 5-6. M. : ZCh MEPhI, 2011.
- Rurukin A.N., Sochilov S.V., Tchaïkovski K.G. Mathématiques 5-6. Un manuel pour les élèves de 6e année de l'école par correspondance MEPhI. M. : ZCh MEPhI, 2011.
- Shevrin L.N., Gein A.G., Koryakov I.O., Volkov M.V. Mathématiques : Manuel-interlocuteur pour les 5-6 années du secondaire. M. : Éducation, Bibliothèque des professeurs de mathématiques, 1989.
- Math-prosto.ru ().
- Youtube().
- School-assistant.ru ().
- Allforchildren.ru ().
Devoirs
Dans cet article, nous traiterons ajouter des nombres avec des signes différents. Ici, nous donnerons une règle pour ajouter des nombres positifs et négatifs, et considérerons des exemples d'application de cette règle lors de l'ajout de nombres avec des signes différents.
Navigation dans les pages.
Règle pour additionner des nombres avec des signes différents
Les nombres positifs et négatifs peuvent être interprétés respectivement comme propriété et dette, tandis que les modules de nombres indiquent le montant de la propriété et de la dette. Ensuite, l’addition de nombres avec des signes différents peut être considérée comme l’addition de biens et de dettes. Il est clair que si la propriété est inférieure à la dette, alors après compensation il y aura une dette, si la propriété est supérieure à la dette, alors après compensation il y aura une propriété, et si la propriété est égale à la dette, alors après le règlement, il n'y aura ni dette ni propriété.
Combinons les arguments ci-dessus en règle pour additionner des nombres avec des signes différents. Pour ajouter un nombre positif et négatif, vous devez :
- retrouver les modules des termes ;
- comparer les chiffres obtenus, tandis que
- si les nombres résultants sont égaux, alors les termes d'origine sont des nombres opposés et leur somme est nulle,
- si les nombres résultants ne sont pas égaux, vous devez alors vous rappeler le signe du nombre dont le module est le plus grand ;
- soustrayez le plus petit du plus grand module ;
- Avant le nombre obtenu, mettez le signe du terme dont le module est le plus grand.
- Plus par moins donne moins ;
- Deux négatifs font un affirmatif.
- Convertissez toutes les fractions contenant une partie entière en fractions impropres. On obtient des termes normaux (même avec des dénominateurs différents), qui sont calculés selon les règles évoquées ci-dessus ;
- En fait, calculez la somme ou la différence des fractions résultantes. En conséquence, nous trouverons pratiquement la réponse ;
- Si c'est tout ce qui était requis dans le problème, nous effectuons la transformation inverse, c'est-à-dire On se débarrasse d'une fraction impropre en mettant en évidence la partie entière.
La règle énoncée réduit l'addition de nombres de signes différents à la soustraction d'un nombre plus petit à un nombre positif plus grand. Il est également clair qu'en additionnant un nombre positif et un nombre négatif, vous pouvez obtenir soit un nombre positif, soit un nombre négatif, soit zéro.
Notez également que la règle d'addition de nombres avec des signes différents est valable pour les entiers, par exemple nombres rationnels et pour des nombres réels.
Exemples d'ajout de nombres avec des signes différents
Considérons exemples d'ajout de nombres avec des signes différents selon la règle discutée dans le paragraphe précédent. Commençons par un exemple simple.
www.cleverstudents.ru
Additionner et soustraire des fractions
Les fractions sont des nombres ordinaires et peuvent également être additionnées et soustraites. Mais du fait qu'ils contiennent un dénominateur, plus règles complexes que pour les entiers.
Considérons le cas le plus simple, lorsqu'il existe deux fractions avec mêmes dénominateurs. Alors:
Pour additionner des fractions avec les mêmes dénominateurs, vous devez additionner leurs numérateurs et laisser le dénominateur inchangé.
Pour soustraire des fractions avec les mêmes dénominateurs, vous devez soustraire le numérateur de la seconde du numérateur de la première fraction, et encore une fois laisser le dénominateur inchangé.
Tâche. Trouvez le sens de l’expression :
Dans chaque expression, les dénominateurs des fractions sont égaux. Par définition de l'addition et de la soustraction de fractions, nous obtenons :
Comme vous pouvez le constater, rien de compliqué : il suffit d'ajouter ou de soustraire les numérateurs, c'est tout.
Mais même dans des actions aussi simples, les gens parviennent à commettre des erreurs. Ce qu’on oublie le plus souvent, c’est que le dénominateur ne change pas. Par exemple, en les additionnant, ils commencent également à s'additionner, ce qui est fondamentalement faux.
Se débarrasser de mauvaise habitude L'addition des dénominateurs est assez simple. Essayez la même chose lors de la soustraction. En conséquence, le dénominateur sera zéro et la fraction perdra (du coup !) son sens.
N'oubliez donc pas une fois pour toutes : lors de l'addition et de la soustraction, le dénominateur ne change pas !
De plus, de nombreuses personnes font des erreurs en ajoutant plusieurs fractions négatives. Il y a une confusion avec les signes : où mettre un moins et où mettre un plus.
Ce problème est également très simple à résoudre. Il suffit de rappeler que le moins avant le signe d'une fraction peut toujours être transféré au numérateur - et vice versa. Et bien sûr, n’oubliez pas deux règles simples :
Regardons tout cela avec des exemples précis :
![]()
Dans le premier cas, tout est simple, mais dans le second, ajoutons des moins aux numérateurs des fractions :

Que faire si les dénominateurs sont différents
Ajouter directement des fractions avec différents dénominateurs c'est interdit. En tout cas, cette méthode m'est inconnue. Cependant, les fractions originales peuvent toujours être réécrites pour que les dénominateurs deviennent les mêmes.
Il existe de nombreuses façons de convertir des fractions. Trois d'entre eux sont abordés dans la leçon « Réduire des fractions en dénominateur commun", nous ne nous y attarderons donc pas ici. Regardons quelques exemples :
![]()
Dans le premier cas, on réduit les fractions à un dénominateur commun en utilisant la méthode des « entrecroisés ». Dans la seconde, nous chercherons le CNO. Notez que 6 = 2 · 3 ; 9 = 3 · 3. Les derniers facteurs de ces développements sont égaux et les premiers sont relativement premiers. Par conséquent, LCM(6, 9) = 2 3 3 = 18.

Que faire si une fraction a une partie entière
Je peux vous plaire : les dénominateurs différents dans les fractions ne sont pas le plus grand mal. Beaucoup plus d'erreurs se produisent lorsque la partie entière est mise en évidence dans les fractions additionnelles.
Bien sûr, il existe ses propres algorithmes d'addition et de soustraction pour de telles fractions, mais ils sont assez complexes et nécessitent une longue étude. Meilleure utilisation diagramme simple, donnée ci-après:
Règles de transition vers fractions impropres et la sélection d'une pièce entière sont décrits en détail dans la leçon « Qu'est-ce que fraction numérique" Si vous ne vous en souvenez pas, assurez-vous de le répéter. Exemples:
Tout est simple ici. Les dénominateurs à l'intérieur de chaque expression sont égaux, il ne reste donc plus qu'à convertir toutes les fractions en fractions impropres et à compter. Nous avons:

Pour simplifier les calculs, j'ai sauté certaines étapes évidentes dans les derniers exemples.
Une petite note sur les deux derniers exemples, où les fractions avec celles en surbrillance sont soustraites partie entière. Le moins avant la deuxième fraction signifie que c'est la fraction entière qui est soustraite, et pas seulement sa partie entière.
Relisez cette phrase, regardez les exemples - et réfléchissez-y. C'est là que les débutants admettent grande quantité les erreurs. Ils adorent confier de telles tâches à essais. Vous les rencontrerez également à plusieurs reprises dans les tests de cette leçon, qui sera publiée prochainement.
Résumé : schéma général de calcul
En conclusion, je donnerai algorithme général, qui vous aidera à trouver la somme ou la différence de deux fractions ou plus :
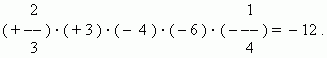











Recette de kebab de Lula sur le grill
Délicieuse okroshka au poulet - vidéo
La prière d'une fille pour le mariage
Prières pour aider avec les problèmes et les ennuis au travail
Comment se débarrasser d'une mauvaise amitié ?